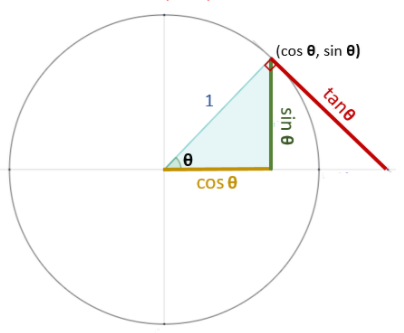
Los conceptos de seno, coseno y tangente surgieron originariamente con los Triángulos Rectángulos y es a lo que se llamaba «Razones Trigonométricas», pero luego esta idea evolucionó en el «mundo» de las funciones, pasando a llamarse «Funciones Trigonométricas», que nos permiten trabajar sin restricciones de ningún tipo.
La definición original de dónde vienen estos conceptos surgió al trabajar con triángulos rectángulos y con los ángulos agudos de estos, es decir, cuando estudiamos trigonometría en el colegio a través de triángulos, estos deben ser rectángulos y al calcular el seno de un ángulo de ese triángulo, siempre es de uno de los ángulos agudos de este.
Para ángulos que no son agudos -mayores de 90º- ya esto no vale y para entenderlo tenemos que pasar al mundo de las funciones trigonométricas, las cuales se definen de otra forma a partir de una circunferencia en los ejes cartesianos.
Ya que las explicaciones son análogas o muy parecidas en todos los casos, vamos a centrarnos en el caso del seno para no hacer muy repetitivas las siguientes explicaciones.
Definición utilizando Triángulos:
El seno de un ángulo es el cateto opuesto partido por la hipotenusa, pero ojo, hay una limitación y es que esta definición sólo «sirve» para ángulos agudos en triángulos rectángulos.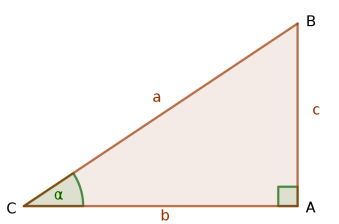
$sin(\alpha) = \frac{c}{a}$
$cos(\alpha) = \frac{b}{a}$
$tan(\alpha) = \frac{c}{b}$
Como vemos son fracciones, por eso se llaman «Razones Trigonométricas»
Definición utilizando funciones.
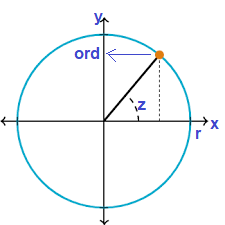
Dada una circunferencia de radio «r» centrada sobre un eje de coordenadas -con su eje «x» o de abscisas y su eje «y» o de ordenadas-, sobre ella puedo marcar un punto.
La función sen(z), por definición, es la ordenada / radio de la circunferencia, es decir, en nuestro dibujo sería $\frac{ord}{r}$
Nota: cuando el radio vale 1, sen(z)= valor de ese punto en el eje de ordenadas.
El sen(z) es una función en donde el valor de entrada z es un ángulo.
Nota: El coseno es lo mismo, pero en lugar de con la ordenada, cogemos la abscisa.
Vamos a recapitular lo visto hasta ahora:
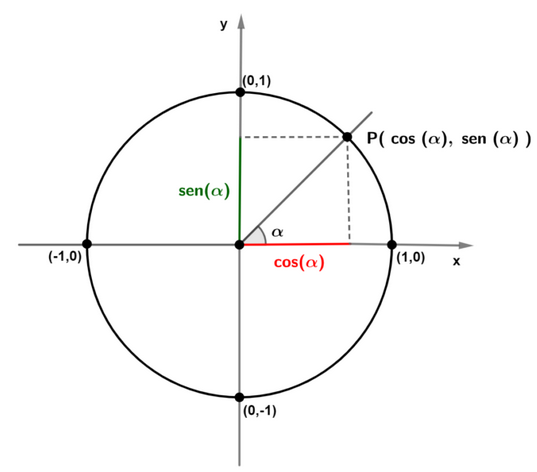
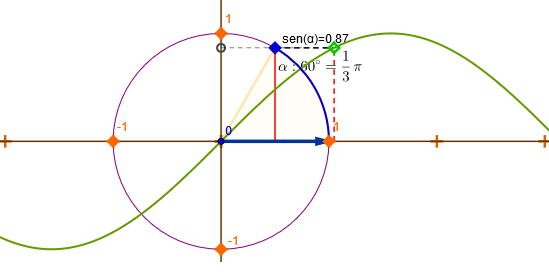
Sobre un círculo de radio 1 (vamos a simplificarlo a 1), en el que marcamos un punto «P», el $\sin(\alpha)$ seno del ángulo $\alpha$ que se forma al unir el origen con ese punto «P», es el valor de la coordenada de ordenadas de ese punto.
Pero esto es pensando en $\alpha$ como un ángulo medido en grados.
Lo que ocurre es que cuando pensamos en la funcion seno como una función de variable real, el valor de $\alpha$ tiene que ser un valor real $\mathbb{
Antes de seguir, vamos a hacer un inciso para recordar un par de cosas:
a) Arco de una Circunferencia:
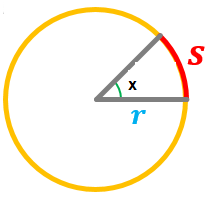
Trabajando en radianes se cumple que, la longitud del arco S en una circunferencia, conociendo el radio r y el ángulo $\alpha$ que forman los dos radios, es:
$S=r \cdot \alpha$
Es decir, si el radio es 1, como es la situación en la que nos encontramos, cuando pensamos en radianes, el ángulo $\alpha$ coincide con la longitud del arco.
No viene mal repasar el término radian sobre el que ya escribí en la web.
b) Función Inversa:
Si tenemos una función $f$ que al recibir como argumento una x, el resultado de la función es un valor y, es decir, $f(x)=y$
Llamamos función inversa de f, y la denotamos como $f^{-1}$ a la función que si recibe como argumento la y nos devuelve la x, es decir $f^{-1}(y)=x$
Nota: esto es sólo una notación para denotar a la función inversa y nada tiene que ver con $\frac{1}{f}$
Una función tiene inversa si es monótonamente creciente o monótonamente decreciente, porque de no ser así, por ejemplo, en una parábola, para dos puntos $x_1$ y $x_2$ distintos, les podría corresponder el mismo valor $y$ y en ese caso, no puede haber función inversa porque esta no sabría si devolver $x_1$ o $x_2$
Pero a nosotros nos han dicho siempre que la función inversa del seno es el arcoseno y viendo su gráfica podemos observar que y=sen(x) no admite inversa, Lo que ocurre es que nos solemos quedar con el dominio $[\frac{-\pi}{2}, \frac{\pi}{2}]$ y aqui la función seno sí que tiene inversa
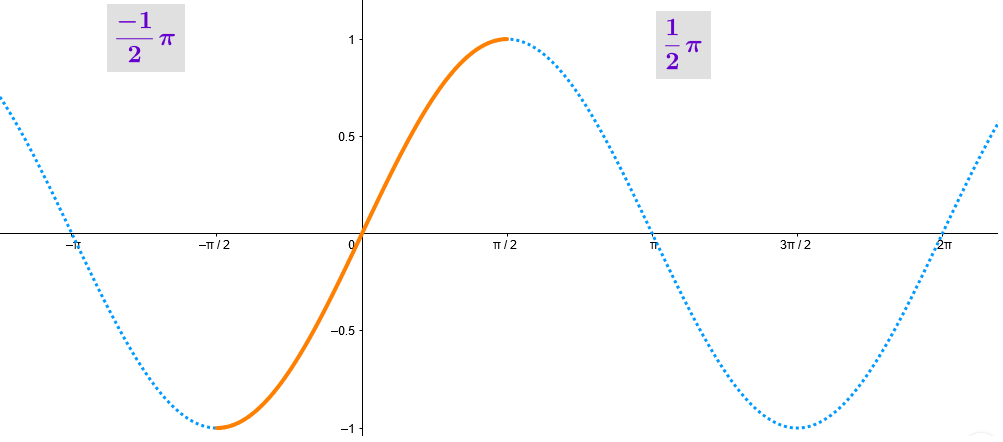
Es decir, si tenemos que $f(x)=\sin(x)=y$
$\arcsin (y)=x$
Antes hemos visto que fijando el radio de una circunferencia a 1 a x lo podemos ver como un arco.
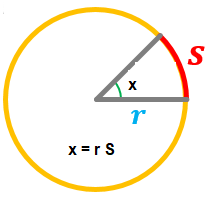
x en radianes es igual al arco S, no es intuitivo, pero es así.
A la función seno, le doy un arco $x$ y me devuelve $y$.
$f(x)=sen(x) =y$
Y el $\arcsin(y)$ lo podemos leer como «el arco cuyo seno es y» o «el ángulo medido en radianes cuyo seno es y»
Y ya para terminar con algo más ligero, ¿para qué sirve la trigonometría?, pues para mil cosas, por ejemplo, una sencilla es medir la altura de un edificio o un árbol sin necesidad de subir a su punto más alto.
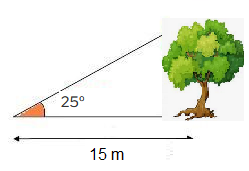
conociendo un ángulo y uno de los lados del triángulo, con trigonometría podemos calcular el resto de valores de los lados y ángulos de ese triángulo rectángulo.