Es uno de los considerados siete problemas de matemáticas del milenio y para los que el Instituto Clay de Matemáticas ha ofrecido un millón de dólares a quien lo resuelva, ¿en qué consiste?.
Los siete problemas del milenio son:
- El problema de P frente a NP.
- La conjetura de Hodge.
- La conjetura de Poincaré.
- La hipótesis de Riemann.
- Yang-Mills y el salto de masa («mass gap»)
- Las ecuaciones de Navier-Stokes.
- Conjetura de Birch y Swinnerton-Dyer.

Hasta la fecha, el único que ha sido resuelto ha sido «la Conjetura de Poincaré», la resolvió el matemático ruso Grigori Perelman. Por esta demostración le fue concedida en 2006 la Medalla Fields (el Nobel de las Matemáticas), pero no acudió a recogerla a Madrid, rechazando también el premio en metálico. De igual forma, rechazó el millón de dólares del Instituto Clay por haber demostrado uno de los considerados problemas del milenio. Una persona realmente increíble en un mundo tan materialista.
Veamos en qué consiste el problema P vs NP tratando de explicarlo de una forma sencilla.
Podemos clasificar los problemas en dos grandes grupos:
Problemas de tipo P: Son los que se resuelven en un tiempo polinómico. Un polinomio sabemos que es una función del estilo
$P(x)=a_n x^n+a_{n-1} x^{n-1}+…+a_1 x^1+a_0 x^0$
El caso más sencillo sería un polinomio de grado 1 $ax+b$ que sería una recta, de grado dos $ax^2+bx+c$ que seria una parábola, etc.
En cualquier caso, siempre sería un tiempo finito en el que un ordenador podría resolver el problema.
Problemas de tipo NP: Son los problemas No Polinómicos.
Estos son los problemas que «no convergen» de forma polinómica, no sabemos lo que el ordenador va a tardar en resolverlo, ya que podríamos decir que el algoritmo funciona un poco «a lo loco», estos son los algoritmos o problemas que no nos gustan, el ordenador puede tirarse días o meses hasta encontrar la solución.
El problema P vs NP se pregunta ¿son los problemas P igual a los problemas NP?, ¿son lo mismo?
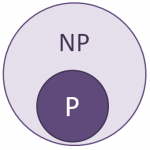
Los problema NP ya incluyen a los P, si se pude resolver en un tiempo infinito, pues con más razón se pueden resolver en un tiempo finito.
A día de hoy no sabemos la respuesta.
Veamos un ejemplo: Para calcular la raíz cuadrada de un número hay un algoritmo que me dice como calcularla, es el que hemos aprendido en el colegio y que casi todos ya hemos olvidado.
Está explicado muy bien en el cortito video de este enlace.
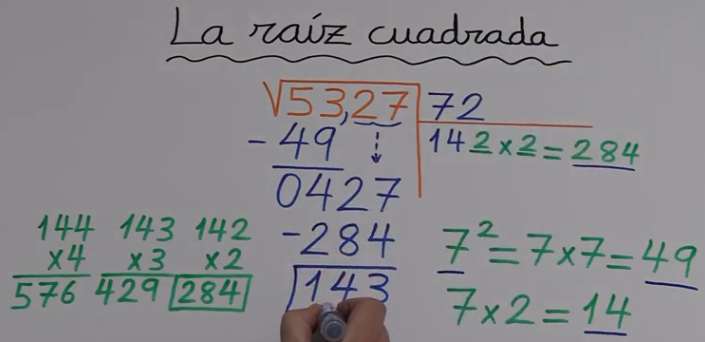
Este es un algoritmo No Polinómico, no es nada sencillo de hacer por un ordenador, no sabemos lo que este va a tardar en resolver la raíz cuadrada de un número verdaderamente grande, la raíz cuadrada de 5327 va a ser rápido, pero si lo quiero calcular para un número muy, muy grande de miles de millones, la cosa cambia.
$\sqrt m=n \text{ si } n^2=m$
$\sqrt 9 =3 \text{ porque } 3^2=9$
Si quiero obtener la $\sqrt m$, puedo intentar coger números n y elevarlos al cuadrado, y el que encaje con m (sin pasarme), esa será la raíz. Esta sería una resolución polinómica de forma que nos permitiría resolver el problema de forma más sencilla y habríamos pasado de un problema que era NP a un problema que ahora es P.
¿Son todos los problemas así?, esta es la gran pregunta, ¿P = NP es completo?.
He ahí la cuestión.

