La genética es una rama de la biología en la que se utilizan mucho las matemáticas. Características hereditarias como el color de nuestros ojos, si somos diestros o zurdos, el color del pelo, etc., viene determinado por los factores «alelos» de nuestros genes y en todo esto tiene mucho que ver la Probabilidad matemática.
Vamos a tratar de ver aquí una versión reducida, de cómo funciona el color de ojos en la herencia genética que recibimos de nuestros padres, pero vamos a hacer primero una breve introducción sobre lo que marca el color de los ojos.
El color de ojos está determinado por dos genes en los cromosomas 15 y 19 respectivamente.
El gen del cromosoma 15 con los factores «alelos» A y a, marca el que tengamos los ojos marrones o claros. La presencia de al menos un alelo «A» implica que los ojos sean oscuros y la presencia de los dos «aa» implica que los ojos sean claros «azules o verdes».
Es decir:
aa: Da lugar a ojos claros
AA: Da lugar a ojos oscuros
Aa: Da lugar a ojos oscuros
aA: Da lugar a ojos oscuros.
Al factor «A» se le llama «dominante» y al factor «a» recesivo.
El gen del cromosoma 19, marca en las personas que tienen los ojos claros «aa» si estos son azules o verdes – Las personas que ya tengan un alelo A en el primer gen, tiene los ojos oscuros sea la que sea la combinación en el segundo gen.
Este segundo gen tiene dos alelos, C y c, siendo dominante el color verde de ojos. Así, si en este gen tenemos al menos una C, es decir CC, cC o Cc, el color de ojos será verde, y si tenemos los dos alelos «cc» el color de ojos será azul.
Tras esta pequeña introducción, vamos a centrarnos en un caso básico en el que únicamente vamos a tener en cuenta dos factores o alelos, A y a de forma que:
A: Es el factor de los ojos marrones y es el dominante.
a: Es el factor de los ojos azules y es el recesivo.
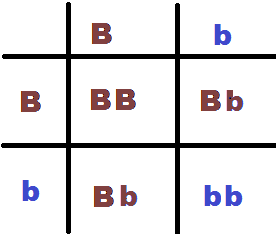
Como estos factores aparecen en pares, pueden darse las siguientes combinaciones de genotipos: aa, aA, Aa y AA (aA y Aa son iguales) y toda persona tiene uno de estos genotipos que le determina el color de ojos.
aa implica tener los ojos azules y el resto de los casos que tienen al menos un factor A, tienen los ojos marrones.
Vamos a hacer un ejercicio muy sencillo para terminar de entenderlo antes de hacernos la pregunta principal de esta entrada.
En los seres humanos, el color marrón de ojos «A» es dominante sobre el color azul «a». Un hombre con los ojos marrones y una mujer con los ojos azules tienen dos hijos, uno con los ojos marrones y otro con los ojos azules. ¿Cuáles son los genotipos de padres e hijos?:
Como tienen un hijo de ojos azules, el padre tiene que haber transmitido un gen a pero como además tiene los ojos marrones, el padre es Aa
La madre y el hijo de ojos azules tiene ambos el genotipo aa.
El hijo de ojos marrones, al tener una madre de ojos azules, tiene que ser Aa.
Una vez dicho esto, la pregunta que podemos hacernos es:
¿Acabará el color de ojos marrón dominando el color de los seres humanos y desaparecerá el color azul de ojos?
Supongamos una población con la proporción de genotipos 1:1:3, o dicho de otra forma
20% es aa
20% es aA
60% es AA
| aa | aA | AA AA AA |
En este caso, la probabilidad de transmitir el factor «a» es $\frac{3}{10}$ (0,3) y la probabilidad de transmitir el factor «A» es del $\frac{7}{10}$ (0,7).
La probabilidad de que el genotipo «aa» aparezca en la siguiente generación es que se transmita «a» y que se transmita «a», es decir, $\frac{3}{10} \cdot \frac{3}{10}=0,09$
Tenemos esto casos:
| a | A | |
| a | aa $\frac{3}{10} \cdot \frac{3}{10}=0,09$ | aA $\frac{3}{10} \cdot \frac{7}{10}=0,21$ |
| A | Aa $\frac{7}{10} \cdot \frac{3}{10}=0,21$ | AA $\frac{7}{10} \cdot \frac{7}{10}=0,49$ |
Los genotipos aA y Aa son idénticos, por lo que la probabilidad de que esto ocurra es $0,21+0,21=0,42$
Es decir, partiendo de un 20% – 20% – 60% en la siguiente generación hemos llegado a 9% (aa)- 42% (aA) y 49%(AA), o dicho de otra forma, como A es dominante, el 9% de la población tendrá los ojos azules y el resto marrones.
Si tras esta segunda generación vuelve a producirse otro apareamiento de forma aleatoria, ¿qué ocurriría?
La proporción de factores «a» que se va a transmitir es
$0,09+\frac{1}{2}\cdot 0,42=$0,3
La proporción de factores «A» que se van a transmitir son
$\frac{1}{2}\cdot 0,42 +0,49=$0,7
que son exactamente las mismas probabilidades de transmisión de estos factores que teníamos al principio y, de hecho, por tanto, el genotipo «aa» no se extingue, sino que sigue estable en e 9% de la población.
Por consiguiente, partiendo de una población 20% – 20% – 60% hemos visto que pasamos a una 9% – 42% – 49% que se estabiliza y ya siempre se mantiene ahí.
9% – 42% – 49% $\rightarrow$ 9% – 42% – 49% $\rightarrow$ … 9% – 42% – 49%
Esto es lo que dice la Ley de Hardy-Weinberg, explica con matemáticas que el gen recesivo no se extingue (el matemático Hardy, el de Ramanujan).
Vamos a ver que esto que hemos visto para una población inicial repartida en 20% – 20% – 60%, se cumple escojamos la proporción inicial que escojamos.
Supongamos una distribución inicial de los genotipos aa, aA y AA como p, 2r y q y las probabilidades de transmisión de «a» p + r y la de «A» r + q (asumimos que ninguno de los genotipos aumenta su mortalidad o decrementa su fertilidad en comparación con los otros dos genotipos).
Para nuestro caso de 20% – 20% – 60% tendríamos
p=0,2
2r=0,2
q=0,6
Las probabilidades de transmisión de los factores a y A son p + r =0,2 + 0,1 = 0,3 y r + q=0,1 + 0,6= 0,7
Para el caso de 10% – 60% – 30%
p + r = 0,1+0,3=0,4 (probabilidad de transmisión de a)
r + q = 0,3+0,3=0,6 (probabilidad de transmisión de A)
De modo que la siguiente generación tendría la siguiente distribución de genotipos 16% – 48% – 36% ya que
Tenemos estos casos:
| a | A | |
| a | aa $0,4 \cdot 0,4=0,16$ | aA $0,4 \cdot 0,6=0,24$ |
| A | Aa $0,6 \cdot 0,4=0,24$ | AA $0,6 \cdot 0,6=0,36$ |
Si continuamos haciendo el mismo ejercicio vemos que ya siempre se mantienen estas probabilidades de transmisión de 0,4 y 0,6 permaneciendo constantes.
10% – 60% – 30% $\rightarrow$ 16% – 48% -36% $\rightarrow$ 16% – 48% -36% $\rightarrow$… 16% – 48% -36%
El 16% de la población tendrá los ojos azules y el 48+36=84% tendrá los ojos marrones porque A es dominante en el genotipo aA.
Las proporciones se mantienen iguales generación tras generación sea cual sea la distribución inicial. El gen dominante A no acaba por dominarlo todo como podría parecer en un principio.