Las integrales múltiples $\iiiint_V \mu(t,u,v,w) \,dt\,du\,dv\,dw$ tienen sentido sobre todo con funciones de más de una variable independiente. ¿Para qué utilizamos las integrales múltiples?, en esta entrada veremos algunas aplicaciones de este tipo de integrales poniendo el énfasis en las dobles.
Antes de empezar a hablar de las integrales múltiples, hagamos un rápido recordatorio sobre funciones de varias variables y sus derivadas, ya que luego nos vendrá muy bien para entender mejor las integrales.
Muchas fórmulas que conocemos son funciones de dos o más variables, veamos algún ejemplo:
- Fórmula de la fuerza que interviene en el movimiento
$F=m\cdot a$
F: Fuerza, m: masa, a: acelaración
esta fórmula, con la notación/variables habituales que utilizamos en matemáticas sería $z=f(x,y)= xy$
- Volumen de un cilindro circular recto
$V=\pi r^2 h$
V: volumen, r: radio, h: altura.
Esta fórmula en matemátias sería la función $z=f(x,y)=\pi x^2 y$
De igual forma podemos tener fórmulas con «n» variables, por ejemplo
$w=f(x,y,z)=x+3y-2z$ es una fórmula o funcion con tres variables independientes.
Cuando hablamos de funciones de varias variables, suele surgir la pregunta de ¿cómo se va a ver afectada la función por una variación de una de sus variables independientes?, podemos responder a esta cuestión considerando cada vez una variable independiente y dejando el resto como variables constantes. Si quisiésemos determinar la razón de cambio de una función «f» con respecto a una de sus variables independientes, esto nos recuerda al concepto de derivada. Podríamos hacerlo derivando la función con respecto a esa variable dejando el resto de variables como constantes. A esto se le llama derivada parcial de f respecto a la variable independiente elegida y se denota así:
Sea z=f(x,y), las derivadas parciales $f_x$ y $f_y$ se denotan
$\frac{\partial } {\partial x} f(x,y) =\frac{df(x,y)}{dx}=f_x(x,y)=z_x=\frac{\partial z } {\partial x} $
$\frac{\partial } {\partial y} f(x,y) =\frac{df(x,y)}{dy}=f_y(x,y)=z_y=\frac{\partial z} {\partial y} $
Las derivadas parciales primeras evaluadas en el punto (a,b) se denotan
$f_x(a,b)=\frac{\partial z } {\partial x} |_{(a,b)}=\frac{\partial z } {\partial x} | _{a}^{b}$
$f_y(a,b)=\frac{\partial z } {\partial y} |_{(a,b)}=\frac{\partial z } {\partial y} | _{a}^{b}$
Al igual que se pueden derivar funciones de varias variables con respecto a una variable manteniendo el resto de variales constantes, pues igualmente podemos integrar funciones de varias variables mediante un procedimiento parecido.
Si tenemos la derivada parcial de la función $f$ respecto a $x$ siguiente
$f_x(x,y)=2xy$, considerando a $y$ constante, podríamos integrar con respecto a x de la siguiente forma $\int dx$ para obtener la función primitiva:
$f(x,y)=\int 2xy dx=y \int 2x dx=y x^2+C(y)$
La constante de integración es realmente una función que depende de y.
Con estos mimbres, ya podemos ponernos a ver las integrales múltiples.
En la entrada titulada «¿Para qué sirven las integrales?», ya vimos que una utilidad de estas (las integrales simples) era la de calcular el área de una región plana. Ahora vamos a ver que esta es también una utilidad de las integrales dobles para funciones de una única variable independiente.
Consideremos la región R limitada por $a \le x \le b, g_1(x) \le y \le g_2(x)$. Si recordamos lo que vimos, el área R se podía calcular como
Área de R= $\int_{a}^{b}[g_2(x)-g_1(x)] dx$
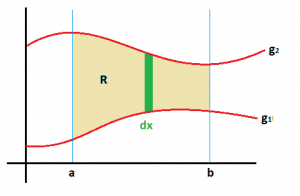
Utilizando el segundo teorema fundamental del cálculo, podemos reescribir el integrando $g_2(x)-g_1(x)$ como una integral definida. Si consideramos x fija y hacemos que la y varíe entre $g_1(x)$ y $g_2(x)$, tenemos:
$\int_{g_1(x)}^{g_2(x)}dx =y | _{g_1(x)}^{g_2(x)} = g_2(x)-g_1(x)$
Por lo tanto, podemos escribir el área de la región R como una integral doble (integral iterada).
$\int_{a}^{b}\int_{g_1(x)}^{g_2(x)}dydx$
Si la región R estuviese delimitada como en el siguiente gráfico, el razonamiento sería similar.
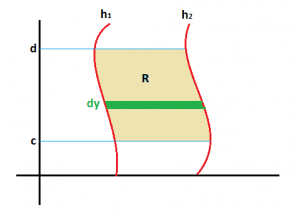
Área de R =$\int_{c}^{d}\int_{h_1(y)}^{h_2(y)}dxdy$
Vamos a ver un ejemplo de cálculo de área utilizando integrales dobles.
Hallemos el área limitada por las siguientes curvas: $y-x^2=2 \text{ y } y+x^2=5$
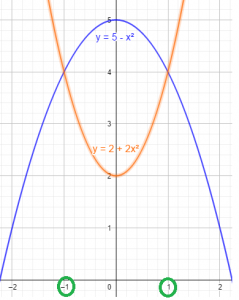
Despejamos $y$ en ambas funciones
$y=2+2x^2 \text{ , } y=5-x^2$
Igualamos para obtener los puntos de intersección de ambas funciones
$2+2x^2 = 5-x^2$
$2x^2+x^2=5-2$
$x^2=1$
$x=\pm \sqrt 1$
$x=\pm 1$
Según lo que hemos visto de teoría, el área de la región comprendida entre ambas funciones utilizando integrales dobles sería:
Área =$\int_{-1}^{1}\int_{2+2x^2}^{5-x^2}dydx$
El orden dydx es debido a que -1 y 1 son los límites de integraión de la variable x mientras que $2+2x^2 \text{ y } 5-x^2$ son los límites de integración de la variable y, i.e. la integral que está más adentro se corresponde con el diferencial que está más adentro y la integral que está más afuera se corresponde con el diferencial que está más afuera.
Área=$\int_{-1}^{1}\int_{2+2x^2}^{5-x^2}dydx = \int_{-1}^{1} [ \int_{2+2x^2}^{5-x^2}dy ] dx = \int_{-1}^{1} [ \int_{2+2x^2}^{5-x^2} 1 dy ] dx $
La integral de 1 respecto a dy es y
=$\int_{-1}^{1} y | _{2+2x^2}^{5-x^2} dx =\int_{-1}^{1}[ (5-x^2)(2+2x^2)]dx=\int_{-1}^{1} [3-3x^2 ]dx = 3x-\frac{3x^3}{3} | _{-1}^{1} $
Sustituyendo los límites de integración queda lo siguiente
=$[3(1)-\frac{3(1)^3}{3}]- [3(-1)-\frac{3(-1)^3}{3}]=4$
El área es 4 metros cuadrados, o la unidad que estemos tratando.
Volúmenes con integrales dobles.
El proceso de obtención de la integral definida en un intervalo consiste en el cálculo del límite del área de distintos rectángulos que se ajustan al área que queremos calcular (esto ya lo vimos en la entrada «¿Para qué sirven las integrales? ».
Un proceso similar puede seguirse para definir una integral doble de una función de dos variables en una región R del plano.
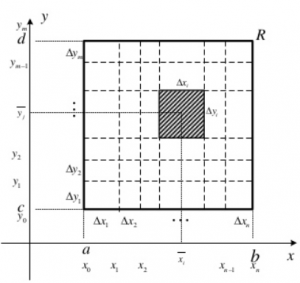
Vamos a trabajar con funciones de dos variables (y aquí está la clave, funciones de dos variables), por ejemplo la función $z=f(x,y)$ definida sobre la región R siguiente:
Aunque no lo vamos a ver aquí, podríamos definir integrales triples en regiones sólidas, integrales de líneas sobre curvas e integrales de superficie sobre superficies.
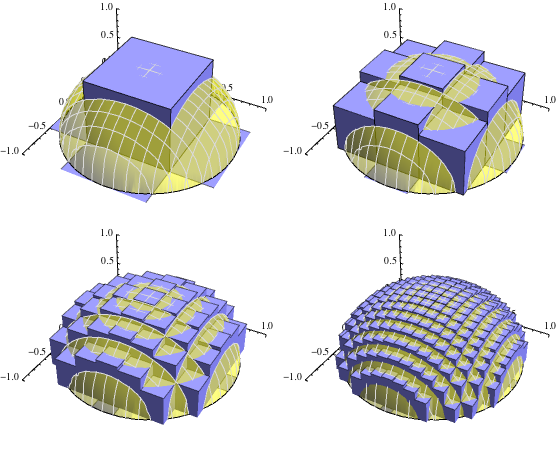
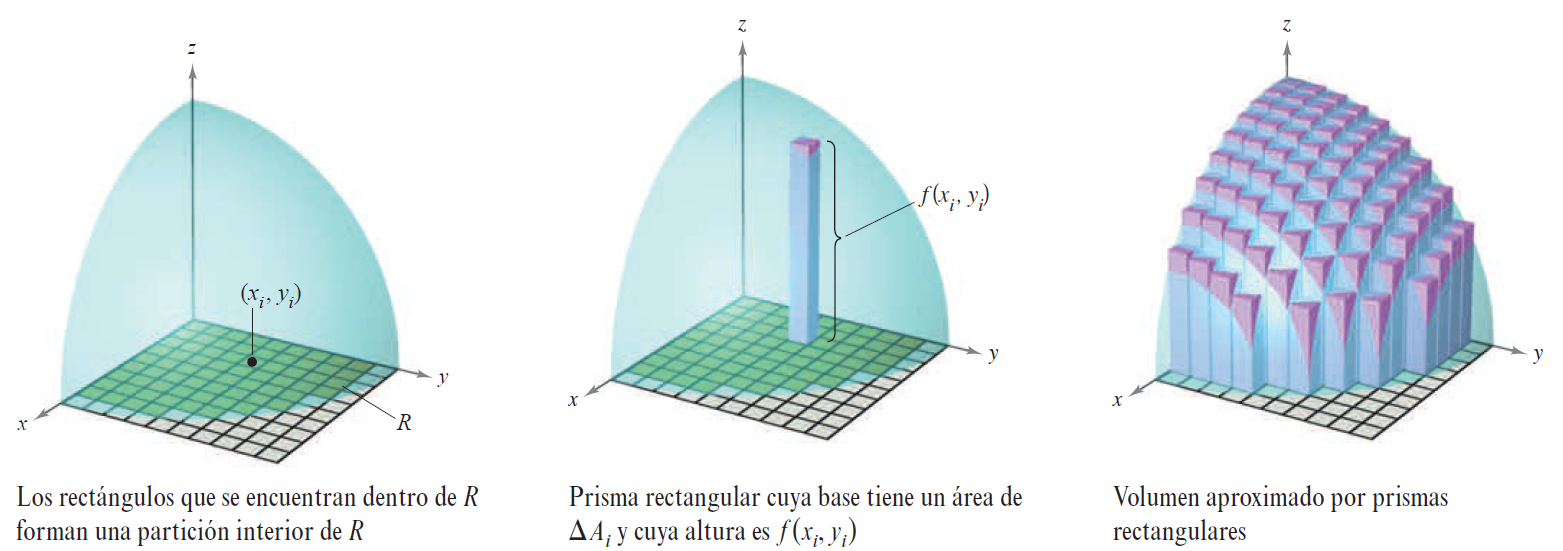
En todos los casos seguimos un modelo que consiste en partir la región R en subregiones más pequeñas, obtener el valor de la función en un punto cualquiera de estas subregiones o subcuadrados y tomar el límite de la suman de Riemann que obtenemos.
Cosideremos una función continua f tal que $f(x,y) \ge 0, \forall (x,y) \in \text{ la región R en el plano xy en donde } a \le x \le b, c \le y \le d$
Vamos a calcular el volumen de la región sólida situada entre el plano xy y la función $z=f(x,y)$.
Haciendo particiones (no tienen por qué ser idénticas) en la región R
$\Delta x_i$
$\Delta x_i = x_{i+1} – x_i $
$ \Delta y_i = y_{i+1}-y_i$
Llamo $\overline{x}_{ij}=(\overline{x}_i, \overline{y}_j)$
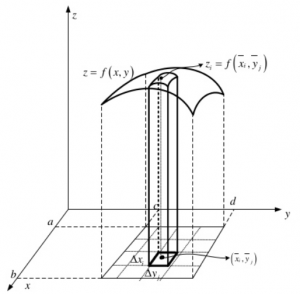
Queremos hacer muy pequeñitos los cuadrados (así el cálculo del volumen de la figura sólida será más exacto), así que calculamos el límite
$\lim_{\Delta x \to 0, \Delta y \to 0} \sum_{j=1}^{m} \sum_{i=1}^{n} f(\overline x_{ij}) \Delta x_i \Delta y_j = \iint_{R} f(x,y) dxdy$
Esto me da el volumen porque $\Delta x_i \Delta y_j $ es el área de la base y $f(\overline x_{ij})$ es la altura del paralelepípedo.
Veamos un ejemplo:
Calcular el volumen del sólido limitado por el paraboloide $z=4-x^2-2y^2$ y el plano xy
Haciendo z=0, vemos que la base de la región en el plano xy es la elipse $x^2+2y^2=4$
Esta elipse tiene la base
$-\sqrt{\frac{4-x^2}{2}} \le y \le \sqrt{\frac{4-x^2}{2}} $
$-2 \le x \le 2$
Por lo que el volumen es:
Volumen=$\int_{-2}^{2}\int_{-\sqrt{\frac{4-x^2}{2}}}^{\sqrt{\frac{4-x^2}{2}}}(4-x^2-2y^2)dydx$
Que podemos calcularlo puesto que sabemos hacer integrales dobles.