Yoli y Nico deciden ir a pasar el día al pueblo, el viaje de ida lo hacen a una velocidad media de 80km/h. Tras pasar un día agradable rodeados de naturaleza, por la tarde se vuelven a la ciudad, pero encuentran bastante atasco y el regreso lo realizan a una velocidad media de 40 km/h.
¿Cuál fue la velocidad media de todo el viaje?
Muy fácil, sumamos las velocidades y dividimos entre 2, es decir, la velocidad media del trayecto de ese día fue de $\frac{80+40}{2}=60 km/h$
Pues no, error.
Fue de 53 km/h
Esto podemos verlo de dos maneras:
- Utilizando la Física
Todos estudiamos en la asignatura de Física, que la fórmula de la Velocidad Media era $v=\frac{d}{t}$ -fórmula que deriva de una matemática-, es decir, necesitamos conocer la distancia y el tiempo.
Bueno, los matemáticos preferimos ponerlo así:
$\overline{v}=\frac{\Delta x}{\Delta t}$
En nuestro caso no conocemos la distancia, pero no importa porque la solución va a ser la misma independientemente de la distancia puesto que la de ida y vuelta son iguales.
Supongamos que la distancia de ida es de 160 km
La distancia total recorrida ha sido de 160+160=320km
El viaje de ida lo han realizado en 2h
El viaje de vuelta lo han realizado en 4h
La velocidad media ha sido de
$v=\frac{d1+d2}{t1+t2}= \frac{320}{2+4}=53,\overline{3} Km/h$
Siendo formales -y generalizando la distancia.
$v=\frac{d}{t}$, luego $t=\frac{d}{v}$
Sea «e» la distancia de ida
$v=\frac{d}{t}=\frac{2e}{ e/80 +e/40 }=\frac{2}{1/80+1/40}=53,\overline{3} $ km/h
- Utilizando directamente las Matemáticas
Deberíamos haber usado la Media Armónica
Este tipo de media suele utilizarse, principalmente, en velocidades o tiempos de trayectos de igual distancia. No podemos utilizarla si una de las observaciones es 0.
La fórmula de la Média Armónica H de un conjunto de valores $x_1, x_2, … x_n$ es
$H=\frac{n} { \frac{1}{x_1}+\frac{1}{x_2}+…+\frac{1}{x_n} }$
n:Número de elementos sobre los que se calcula la media.
En nuestro ejemplo $\frac{2}{ 1/80 +1/40} = 53,\overline{3}$
¿Cuál es la figura más armónica?
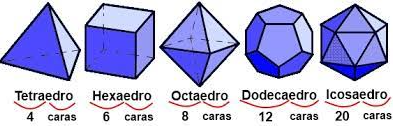
Cómo curiosidad, decir que esta pregunta se la hacían lo griegos cuando observaban los poliedros regulares.
La respuesta es que el Cubo o Hexaedro, ya que el número de vértices es media armónica entre las caras y las aristas y eso no ocurre con el resto de figuras.
Si recordamos la fórmula de Euler C+V=A+2
En este casto tenemos 6 Caras, 8 Vértices y 12 Aristas.
En este caso V=8, C=6, A=12 y la media armónica de las caras y aristas
$H=\frac{2}{1/6 + 1/12}=\frac{2}{ \frac{3}{12} }=\frac{24}{3}=8$
La media armónica es la que nos dice que invirtamos poco a poco en bolsa.
Supongamos que tenemos 8000€ para invertir en bolsa.
Decidimos invertir 2000€ cada trimestre. El último día de cada trimestre el precio de la acción es de:
Q1: 10€
Q2: 4€
Q3: 5€
Q4: 20€
El precio medio -media aritmética- de la acción en este tiempo ha sido $\frac{31}{4}=7,75€$
Si hubiésemos comprado al precio medio de la acción hubiésemos obtenido $\frac{8000}{7,75}=1032,25$ títulos
Al invertir de esta forma:
Q1: $\frac{2000}{10}=200$ títulos
Q1:$\frac{2000}{4}==500$ títulos
Q1: $\frac{2000}{5}=400$ títulos
Q1: $\frac{2000}{20}=100$ títulos
Hemos obtenido 1200 títulos -más que los 1032,25- y a un precio de $\frac{8000}{1200}=6,\overline{6} $ que es el que sale aplicando la media armónica.
Aplicando la fórmula de la media armónica
$H=\frac{4}{1/10 + 1/4 +1/5 +1/20}= 6,\overline{6}$€
La Media Aritmética es la que a todo el mundo se le viene a la cabeza de primeras, porque es la que nos decía la nota media obtenida en el curso cuando teníamos varias a lo largo del mismo. Es el resultado que se obtiene sumando todos los valores de una muestra y dividiéndolo por el número de dichos valores. Otorga el mismo peso o importancia a todos los valores de la muestra. Es el valor que tendrían los datos, si todos ellos fueran igual de importantes.
Lo vimos aquí
No debemos olvidarnos de las medias geométrica y la ponderada.
Media Geométrica
Esta media es la que se utiliza para calcular medias sobre porcentajes.
$\overline{x}=\sqrt[n]{ \prod_{i=1}^{n}x_i }=\sqrt[n]{x_1 \cdot x_2 \cdot \cdot \cdot x_n }$
Siendo:
n: número total de observaciones
$x_i$=cada una de las observaciones, por ejemplo, cada uno de los porcentajes/crecimiento de los beneficios o lo que sea que estemos observando.
Media Ponderada
La media ponderada es aquella que asigna diferentes pesos a los distintos valores sobre los que ésta se calcula.
Se diferencia de la media aritmética en que no les da la misma importancia a todos los valores. De hecho, en realidad la media aritmética es una media ponderada en la que todos los valores son igual de importantes.
Supongamos que para ponele la nota del trimestre a un alumno queremos tener en cuenta
a) Si hace los deberes a diario. Pesaría 15%
b) Participación en clase. Pesaría 10%
c) La nota del examen final. Pesaría el 75% de la nota.
Supongamos que ha sacado en el examen un 8, y le otorgamos un 7,5 en los deberes y un 5 en participación.
La fórmula para calcular la media ponderada es
$W=\frac{ \sum_{n=1}^{n}{x_i\cdot w_i} }{ \sum_{n=1}^{n}w_i}=\frac{x_1\cdot w_1 + x_2\cdot w_2+…+x_\cdot w_n}{w_1+w_2+…+w_n}$
Siendo «n» el número total de observaciones, $x_i$ las observaciones -en este caso las notas- y $w_i$ los pesos.
En nuestro ejemplo la nota sería:
Nota=$\frac{7,5*15+5*10+8*75}{15+10+75}=7,6$
Hay muchas más medias, pero estas son las más importantes -quizás faltaría la media cuadrática para que no se enfadasen los estadísticos.