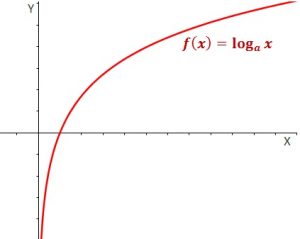
Cuando a mí me enseñaron los logaritmos, no recuerdo que me contasen para qué servían, me explicaron su definición, así como una serie de reglas para poder operar con ellos, es decir, aprendí puro cálculo sin ninguna noción de comprensión de lo que estaba haciendo, ahora lo recuerdo y creo que faltó que esto también me lo enseñasen para poder verle utilidad a todo lo aprendido.
Antes de contar para que sirven, hagamos un breve repaso de ellos, ya que nos ayudará a comprenderlo todo mejor.
Un logaritmo es el exponente al que hay que elevar un número, llamado base, para obtener otro número determinado. El logaritmo en base 10 de 1000 es 3.
$$ \log_{a}b=c \text{ ⇔ } a^c=b$$
$$\text{ siendo por definición } \{b\in\mathbb{R} : b>0\} \text{ y } \{a\in\mathbb{R} \text{-{1}} : a>0\}$$
El método logarítmico fue presentado públicamente por el matemático y teólogo escocés John Napier en 1614, en un libro titulado «Mirifici Logarithmorum Canonis Descriptio» (Descripción de una maravillosa tabla de Logaritmos), en esa época los trabajos científicos se escribían todos en latín. De Napier viene el nombre de logaritmo neperiano (Napierian logarithm o Naperian logarithm).
Es muy importante recordar algunas propiedades de los logaritmos para entender para que sirven:
Logaritmo de un producto.
El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
$$ \log_{b}a\cdot c=\log_{b}a+\log_{b}c$$
Logaritmo de un cociente.
El logaritmo de un cociente es igual al logaritmo del dividendo, menos el logaritmo del divisor.
$$ \log_{b}\frac{a}{c}=\log_{b}a-\log_{b}c$$
Logaritmo de una potencia.
$$ \log_{b}c^n=n\log_{b}c$$
Logaritmo de una raíz
$$ \log_{a}\sqrt[n]{x^{m}} =\frac{m}{n}\log_{a}x$$
El antilogaritmo: El antilogaritmo nos permite a partir de la base y del exponente calcular el argumento (lo contrario que el logaritmo que a partir de la base y el argumento nos da el exponente).
$$ \log_{2}8=3$$ siendo 2 la base, 8 el argumento y 3 el exponente.
Permite a partir de la base y del exponente, obtener el argumento.
antilog 2 3=8
Los logaritmos se emplearon principalmente como una herramienta para poder simplificar multiplicaciones, divisiones y la extracción de radicales cuando teníamos que trabajar con números muy muy grandes.
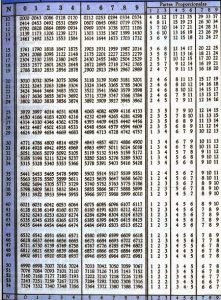
Desde mediados del siglo XX con la expansión de los ordendores de forma más generalizada, esto ya ha perdido algo de sentido puesto que estos hacen esos cálculos grandes de una forma sencilla, pero antes, como los ordenadores no eran tan accesibles, si teníamos que trabajar con cifras muy grandes, la solución era utilizar logaritmos y tablas de logaritmos (así como de tablas de antilogaritmos) en las que poder consultar el valor del logaritmo de un número.
Los logaritmos nos permiten convertir el producto en una suma (primera de las propiedades de los logaritmos que hemos repasado, es más fácil sumar que multiplicar), el cociente en resta (es más fácil restar que dividir), una potencia en una multiplicación y una raíz en una simple división.
Con la existencia de tablas de logaritmos para obtener el logaritmo de un número de forma sencilla (y su antilogaritmo), lo que hacíamos era en lugar de trabajar con números grandes, trabajar con el logaritmo de esos números que eran cosas bastante más pequeñas $$ \log_{10}100000000=8$$ mejor trabajar con el 8 que con 100000000 y al final del proceso calculábamos el antilogaritmo de lo obtenido.
Genial, ¿verdad?
Si se tuviese que hacer la multiplicación de por ejemplo 0.7589547936 por 0.8321474, lo que se haría es calcular su logaritmo, y al final del proceso, volver hacia atrás, es decir, calcular su antilogaritmo. Hoy en día con los ordenadores no tiene sentido, pero antes era esto lo que se hacía.(Fernandez Herce, J.,2010, cuentasycuentos.jorgefernandezherce.es)
$$\text{0.7589547936 lo sustituiría por 7589547936} \cdot 10^{-10}$$
$$\text{0.8321474 lo sustituiría por 8321474} \cdot 10^{-7}$$
Que al final, por la propiedad de los logaritmos se convierte en cuatro sumas de logaritmos muy sencillas.
$$ \log_{10}7589547936 +\log_{10}10^{-10} +\log_{10}8321474+\log_{10}10^{-7} =$$
$$\log_{10}7589547936 -10 +\log_{10}8321474 -7 =$$
$$\log_{10}7589547936 + \log_{10}8321474 -17$$
Los dos primeros logaritmos los miraríamos en tabla y ya tendríamos el resultado, luego el proceso contrario sería mirar en la tabla de antilogaritmos para deshacer la aplicación de la función logarítmica.
Trabajo conseguido. Estupendo.
- Los logaritmos nos dan información sobre cuánto de grande es un número porque me da una idea de los dígitos que tiene. Conocer el número de dígitos me permite estimar el tamaño del producto. Por tanto, esta es otra utilidad de los logaritmos.
- Los logaritmos se utilizan para determinar la antigüedad de restos vegetales y animales si utilizamos el método del carbono 14.
- Se utilizan en psicología en la ley de Weber-Fechner
- Se utilizan en la escala de Richter para reflejar la energía que se desprende en un terremoto. La intensidad de un sismo se calcula en utilizando logaritmos neperianos.
- En Estadística se suelen aplicar en el crecimiento de la población, cuando la poblacion crece muy rápidamente (exponencialmente), para simbolizarlo utilizamos logaritmos,
$$\log_{10}1000000=6$$
$$\log_{10}10000000=7 $$
$$\log_{10}100000000=8 $$
$$\text{ etc.}$$
- En el experimento psicológico de Stenbeg.
- En la Música, en Topología, en Quimica para medir el pH de un producto, etc, es decir, en innumerables situaciones se utilizan los logaritmos.
- En Astronomía los logaritmos son muy usuales, se utilizan para poder medir el brillo y la magnitud de las estrellas.
Todo lo que sean numeros muy grandes, se maneja mejor aplicando logarítmos.