¿Te imaginas que vas conduciendo con el coche hacia un restaurante en el que has reservado para comer, y sabes decidir si aparcar en el hueco que acabas de ver o si apuras un poco más para estar más cerca del destino?
¿Te imaginas que sabes si la novia con la que estás saliendo es la mujer ideal o si tienes que dejarla y buscar otra que será mejor?
¿Te imaginas que sabes elegir correctamente el baño portátil más limpio en fiestas?

¿Cuántas posiciones de un tablero de ajedrez debes analizar antes de realizar un movimiento?
Vamos a ver cómo responder a estas preguntas, y lo más importante, vamos a demostrar matemáticamente que el criterio que vamos a seguir es el más eficiente.
El problema de la dote del Sultán es un problema muy famoso en matemáticas que está englobado dentro de lo que en matemáticas llamamos problemas de parada óptima -que sirven para decidir qué momento es el mejor para parar y maximizar la probabilidad de tener éxito-.
Expliquemos en qué consiste:
Un sultán tiene cien hijas y decide dar la mano de la hija que tiene mejor dote a aquel de sus súbditos que supere la siguiente prueba:
- Las hijas irán pasando de una en una delante del pretendiente, al que se le dirá la dote que lleva consigo cada una de ellas.
- El súbdito sólo podrá casarse con la hija de mayor dote si adivina cuál de ellas es.
- Según se le vayan presentando al pretendiente cada una de las muchachas, se le dirá a este la dote que la acompaña y en ese mismo instante el súbdito deberá decidir si la elige como esposa o si prefiere continuar viendo a la siguiente. Una vez rechazada una de las hijas, la decisión es en firme y no la puede cambiar ni elegir a una de las ya rechazadas.
- Todas las dotes son distintas y el pretendiente no tiene ninguna información previa acerca de su cuantía. Las hijas pueden desfilar delante del pretendiente en cualquier orden.
¿Cuál es entonces la mejor estrategia para superar la prueba?
Vamos a ver el problema con un caso sencillo de tres hijas.
Si elegimos una de las hijas al azar, la probabilidad de acertar con aquella que tiene la mayor dote es $\frac{1}{3}=\frac{\text{casos favorables}}{\text{casos posibles}}$.
Consideremos la siguiente estrategia:
Dejamos pasar a la primera de las hijas (la A) para conocer cuál es su dote, pero la descartamos sea cual sea la dote que tenga.
Dejamos pasar a la siguiente de las hijas (la B), si tiene más dote que la primera, la elegimos, en caso contrario nos quedamos con la tercera.
Siguiendo esta estrategia podemos garantizar un éxito del 50 % -ganamos 3 de 6-, lo cual es mejor que el 33 % ($\frac{1}{3}$) que teníamos si escogemos una de las hija al azar.
| Permutaciones $3!=6$ | Dote | |||||
| A | B | C | 300 | 150 | 5 | |
| A | C | B | 300 | 5 | 150 | |
| B | A | C | 150 | 300 | 5 | |
| B | C | A | 150 | 5 | 300 | |
| C | A | B | 5 | 300 | 150 | |
| C | B | A | 5 | 150 | 300 | |
| Aciertos: | 2 | 3 | 2 | |||
Existe una fórmula matemática -que luego veremos de dónde sale-, según la cual, tendremos que desechar un determinado número de hijas del sultan antes de quedarnos con la que tenga una dote más elevada que la más alta de las desechadas.

Esta fórmula lo que nos dice es que el número de opciones que debemos rechazar «n», debe ser el número natural más próximo al número total de opciones «N», dividido entre el número «e» -N/e-. Es increíble que el número de Euler aparezca aquí.
$n=\frac{N}{e}$
Como el sultán tiene 100 hijas, deberemos dejar pasar $\frac{100}{2,71}=36,9$, i.e., dejaremos pasar a 37 hijas y a partir de ahí, elegiremos aquella cuya dote supere a todas las precedentes (incluyendo las «n» primeras).
Pasemos a ver de dónde sale todo esto.
El problema consiste en calcular el número «n» que maximiza la probabilidad de elegir la dote más alta.
Veamos cuál es la probabilidad de acertar con «N» hijas habiendo rechazado a las primeras «n»:
Acertamos si la de mayor dote está en el puesto n + 1 y esto ocurre con probabilidad $\frac{1}{N}$. También acertamos si la mayor dote está en el puesto n+ k+ 1, lo cuál ocurre con probabilidad $\frac{1}{N}$, y la mayor de las n + k precedentes está entre las «n» primeras, lo que ocurre con probabilidad $\frac{n}{n+k}$.
Por lo tanto, esto ocurre con una probabilidad
$\frac{1}{N} \cdot \frac{n}{n+k}$
La probabilidad de acertar con esta estrategia es la suma de estas probabilidades extendida a todos los posibles valores de «k» así $\forall k \in [0,N-n-1]$
$P_{acertar}= \frac{n}{N}( \frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{N-1})$
Tenemos que encontrar el número «n» que maximiza esta probabilidad.
En Teoría de Números los números armónicos se definen como
$H_n=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$
$P_{acertar}= \frac{n}{N}( H_{N-1}-H_{n-1})$
Euler encontró un valor aproximado a esta serie, al valor de número armónico $H_n$ que es mejor cuanto mas grande sea «n».
$H_n \approx ln(n)+\gamma$, en donde $\gamma$ es la constante de Euler-Mascheroni que vale 0,5772
Utilizando la aproximación de Euler a la probabilidad de acertar obtenemos:
$P_{acertar}= \frac{n}{N}( H_{N-1}-H_{n-1}) = \frac{n}{N}(ln(N-1) + \gamma -ln(n+1)-\gamma)= \frac{n}{N}(-ln(\frac{n-1}{N-1}) $
Cuando tanto N como n son muy grandes, la probabilidad de acertar depende sólo de x= n/N, es decir, de la fracción de hijas rechazadas de antemano:
$P_{acertar}=-xln(x)$
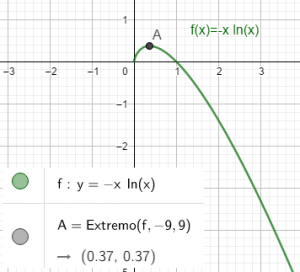
El valor máximo esta función la alcanza para $x=\frac{1}{e}$ (revisar el artículo que escribí sobre derivadas)
$P_{acertar, máximo}=\frac{1}{e}$
La probabilidad de éxito siguiendo esta estrategia será cómo mínimo $\frac{1}{e}$, es decir, 36.8% aunque el número de hijas del sultán creciese hasta infinito.
Curiosamente la máxima probabilidad de acertar coincide con el valor óptimo de x. En realidad, hemos resuelto el problema suponiendo que x puede tomar cualquier valor, pero en la práctica sólo puede tomar valores $x=\frac{n}{N}$, siendo «n» entero. La solución final, siempre aproximada, sería el número natural más próximo a $\frac{1}{e}$, despejando tenemos que $n=\frac{N}{e}$.
Como resumen, recordar que si elegimos una de las 100 hijas del sultan al azar, nuestra probabilidad de acertar es del $\frac{1}{100}$, mientras que si rechazamos a las 37 primeras que se nos presenten, la probabilidad sube por encima del $\frac{37}{100}$.

