En esta entrada vamos a revisar conceptos de estadística y veremos como estos se aplican en el ámbito de los fondos de inversión. Con la estadística, obtenemos información a partir de los datos que tenemos y esto nos permite conocer si el fondo lo está haciendo bien, o si por el contrario lo está haciendo mal en comparación con otros fondos similares.
Cuando un cliente decide comprar un fondo de inversión, tiene que fijarse en varias cosas , entre ellas están el periodo de tiempo que tiene pensado mantener la inversión, el nivel de riesgo dispuesto a asumir, las comisiones que le van a cobrar en el fondo que finalmente elija (comisión de gestión, de suscripción, …), las rentabilidades que ha ido obteniendo el fondo hasta la fecha y varias cosas más entre las que se encuentra el objeto de esta entrada, los datos estadísticos del fondo o al menos algunos de ellos (los más importantes).
Vamos a empezar definiendo estos conceptos estadísticos empezando por alguno fácil que necesitaremos para comprender los demás.
Frecuencia Absoluta $f_i$
Dada una muestra de datos, llamamos frecuencia absoluta de un valor, al número de veces que aparece ese valor y se representa por $f_i$, donde el subíndice i representa a cada uno de los valores.
La suma de las frecuencias absolutas es igual al número total de datos que se representa por N.
$f_1 + f_2 + f_3 + … + f_n = N$
o como decimos los matemáticos
$\sum\limits_{i=1}^n f_i=N$
Frecuencia Relativa $n_i$
Llamamos frecuencia relativa de un valor de una muestra, al cociente de dividir su frecuencia absoluta entre el número total de elementos de la muestra.
Se puede expresar en tanto por ciento y se representa por $n_i$.
La suma de las frecuencias relativas es igual a 1.
$n_i = \frac{f_i}{N}$
$\sum\limits_{i=1}^n n_i=1$
Todo esto como mejor se entiende es con un sencillo ejemplo.
Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29.
Ordenando los datos de menor a mayor podemos pintar una tabla de frecuencias.
$N=31$
| Distintos valores xi | Frecuencias Absolutas fi | Frecuencias Relativas ni |
| 27 | 1 | 0.032 |
| 28 | 2 | 0.065 |
| 29 | 6 | 0.194 |
| 30 | 7 | 0.226 |
| 31 | 8 | 0.258 |
| 32 | 3 | 0.097 |
| 33 | 3 | 0.097 |
| 34 | 1 | 0.032 |
| Total | 31 | 1 |
Ahora vamos a repasar las Medidas de Centralización más comunes.
Media Aritmética $\overline{x}$
La media aritmética es el valor obtenido al sumar todos los datos ($x_i$) y dividir el resultado entre el número total de datos.
El símbolo de la media aritmética es $\overline{x}$
$\overline{x} =\frac{ f_1 x_1 + f_2 x_2 + f_3 x_3+… +f_n x_n}{N} =\frac{\sum\limits_{i=1}^n f_i x_i}{N}$
Ejemplo:
Los pesos de ocho amigos son: 84, 91, 72, 68, 84, 72, 84, 84 y 78 kg (para verlo mejor es preferible ordenar los datos). Hallar el peso medio.
$\overline{x}=\frac{4 \cdot 84+91 +2\cdot 72+68+78}{9}=79,\overline{6} kg$
Moda Mo
Es el valor que tiene mayor frecuencia absoluta, en el ejemplo anterior sería el 84.
Si hay dos modas, la serie de datos se dice que es bimodal. Trimodal si tiene 3 modas, etc.
Mediana Me
Es el valor que ocupa la posición central cuando los datos están ordenados. Ejemplo: Hallemos la mediana de la siguiente serie de números:
3, 5, 2, 6, 5, 9, 5, 2, 8.
Ordenado queda: 2, 2, 3, 5, 5, 5, 6, 8, 9.
Me = 5
La mediana es sobre todo importante tenerla en cuenta si existe algún elemento que pueda distorsionar la muestra.
Ejemplo: Pesos de los alumnos de una clase.
50, 50, 51,51, 51, 53,53,55
Media: La suma de todos los datos / el número de datos . $\overline{x}$ = 51,75 Kg$
Ahora llega un alumno muy rellenito que pesa 200kg y que me va a desvirtuar la media, entonces es mejor utilizar la mediana.
50, 50, 51,51, 51, 53,53,55, 200
Media:$ \overline{x}=\frac{2 \cdot 50 +3\cdot 51+2\cdot 53+55+200}{9}=68,2$
Mediana Me=51 Kg, ya que 50, 50, 51,51, 51, 53,53,55, 200
Repasemos algunas Medidas de Dispersión:
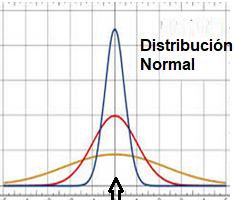
En el siguiente dibujo obtendríamos el mismo valor para la media, mediana y moda (sería la flechita negra), sin embargo vemos que la distribución en los tres casos es muy diferente. La variabilidad de la curva amarilla es muchísimo mayor que la de la curva azul. Si hablásemos por ejemplo de un negocio, en la curva azul las ventas estarían mucho más concentradas que en las otras curvas. La variabilidad no siempre es malo, si hablamos por ejemplo de biodiversidad, pues que haya variabilidad es bueno, sin embargo, en los conceptos de calidad lo que queremos es que la variabilidad se reduzca al máximo.
La primera medida de dispersión que se suele ver es:
Rango o Recorrido R
Es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Se suele hacer valor mayor – valor menor + 1 (para coger el valor del extremos).
Desviación Media DM
La desviación respecto a la media nos da información de lo lejos o cerca que está un dato de los demás datos del conjunto. Se calcula como la diferencia de un dato y la media del resto de los datos $x_i – \overline{x}$
Si en un examen Nicolás ha obtenido un 8 y la media de la clase es de 6’5, la desviación respecto a la media de la nota de Nicolás es 8-6’5=1,5
El signo de la desviación respecto a la media indica si el valor está por encima de la media (signo positivo), o por debajo de la media (signo negativo).
El valor absoluto de la desviación respecto a la media nos indica lo lejos que está el valor de la media. Un valor igual a cero nos indica que el valor coincide con la media, mientras que un valor muy alto con respecto a las demás desviaciones nos informa de que el dato está alejado de los demás datos.
La DM de un conjunto de datos se calcula así:
$DM=\frac{\sum\limits_{i=1}^n f_i \cdot |x_i – \overline{x} |}{N}$
Ejemplo. Calculemos la DM de la distribución 9, 3, 8, 8, 9, 8, 9, 18
Primero calculemos la media $\overline{x}=\frac{3 \cdot 9 +3\cdot 8 +3+18}{8}=9$
Calculamos la $DM=\frac{3 \cdot |9-9| +3\cdot |8-9| +|3-9|+|18-9|}{8}=2,25$
Cuanto mayor es la DM, mayor es la dispersión de los datos.
La desviación media quedó ya en deshuso, sin embargo es la base para el resto de medidas.
Varianza $\sigma^2$
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
$\sigma^2=\frac{\sum\limits_{i=1}^n f_i \cdot (x_i – \overline{x})^2}{N}$
Siguiendo el ejemplo de la distribución anterior
$\sigma^2=\frac{3 \cdot (9-9)^2 +3\cdot (8-9)^2 +(3-9)^2+(18-9)^2}{8}=15$
El problema con la varianza es que si estamos dando la varianza en un resultado, por ejemplo euros, estaríamos hablando de $€^2$ por lo que es una medida que exagera la variabilidad, si estamos comparando $1^2$ contra $100^2$ estaríamos exagerando la diferencia. Debido a esto es por lo que lo que más se utiliza es la siguiente medida:
Desviación Típica $\sigma$ (también llamada Desviación Estándar)
La desviación típica es la medida de dispersión más utilizada, muchísimo más que la DM y la $\sigma^2$, las cuales acabo de explicar realmente porque ayudan a entender mejor como llegamos a la desviación típica/estándar. Es la raíz cuadrada de la varianza (en el caso de los fondos de inversión se suele llamar volatilidad del fondo) y al hacer la raíz cuadrada de algo al cuadrado, pues estamos volviendo realmente a su dimensión.
Su interpretación es muy parecida a la de la DM o la varianza, es decir, mide cómo se separan los datos, una desviación típica alta significa que los datos están dispersos, mientras que un valor bajo indica que los valores son próximos los unos de los otros, y por lo tanto de la media.
$\sigma=\sqrt{\frac{\sum\limits_{i=1}^n f_i \cdot (x_i – \overline{x})^2}{N} }$
La desviación típica podemos entenderla también como un indicador de qué es lo normal.
El siguiente ejemplo lo he tomado de la web disfrutalasmatematicas.com pues me ha parecido muy clarificador y dificil de explicar mejor.
Ejemplo:
Medimos las alturas (hasta los hombros) de los perros de los amigos (en milímetros) y obtenemos
600mm, 470mm, 170mm, 430mm y 300mm.
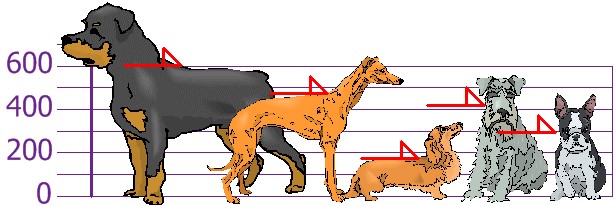
Calculamos la media, la varianza y la desviación típica.
Media $\overline{x} =\frac{(600+470+170+430+300)}{5}=394 mm$
Varanza $\sigma^2=\frac{ (600-394)^2 + (470-394) +(170-394)^2+(430-394)^2 + (300-394)^2}{5}=21704$
Desviación típica $\sigma=\sqrt{21704}=147$
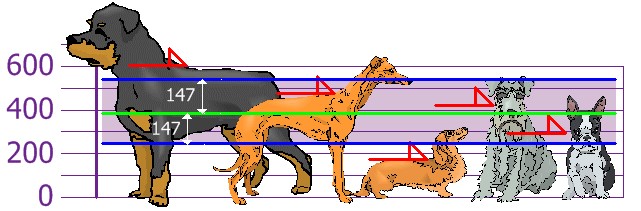
Así que usando la desviación estándar tenemos una manera «estándar» de saber qué es normal, o extragrande o extrapequeño. A la media le sumo por arriba y le resto por debajo la desviación estándar y tengo el tramo de lo que es lo más «normal». Lo normal es que los perros midan 394mm $\pm$ 147 mm.
Los Rottweilers son perros grandes y los perros salchicha son más pequeños de lo normal.
La desviación estándar nos indica también, cómo de dispersos están los datos con respecto a la media. Mientras mayor sea la desviación estándar, mayor será la dispersión de los datos. Veamos un ejemplo clarificador:
Tenemos dos hospitales A y B en los cuales, en ambos el tiempo medio de espera para ser atendido es de 25 minutos.
El hospital A tiene sin embargo una desviación típica de 7 y el hospital B de 15.
En el hospital A, en promedio el tiempo que un enfermo tiene que esperar para ser atendido se separa de la media 7 minutos.
En el hospital B, en promedio el tiempo que un enfermo tiene que esperar para ser atendido se separa de la media 15 minutos.
La dispersión, la variación, la volatilidad de los datos es mucho mayor en la sala de espera de urgencias del hospital B.
Estas medidas de dispersión vistas hasta ahora nos siven para comparar entre dos conjuntos de datos con el mismo tipo de divisa en nuestro caso, es por eso que en estadística se utiliza mucho lo que se llama el Coeficiente de Variación.
Coeficiente de Variación CV
CV=$\frac{\sigma}{\overline x} \cdot 100$
Siendo $\sigma$ la desviación típica y $\overline{x}$ la media.
Lo de multiplicar por 100 es para mostrarlo como un porcentaje.
Esta es ya una medida relativa, ya que si la desviación típica está en euros y la media está en euros, ambas dimensiones se anulan y la medida se queda adimensional. Esto es importante porque permite comparar variables diferentes (podemos hablar de manzanas y peras y comparar las variabilidades de las dos).
En general si la variabilidad es mayor que 20% decimos que esta es alta y si es menor que 20% decimos que es baja y por tanto la distribución sería uniforme.
Una vez hecho este «repaso», vamos a centrarnos ya en los fondos de inversión.
Repasemos las Medidas de Forma
Hay dos tipos de cálculos que podemos hacer aquí en función de si nos fijamos en la forma horizontal o en la forma vertical de las distribuciones.
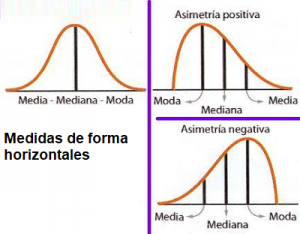
Una medida de forma horizontal nos indica como está distribuidos los datos horizontalmente, es decir, si son simétricos o asimetricos hacia alguno de los lados.
Coeficiente de Asimetría de Fisher CA
$CA_F=\frac{\sum\limits_{i=1}^n f_i \cdot (x_i – \overline{x})^3}{N \sigma^3}$
Siendo $\overline{x}$ la media y $\sigma$ la desviación típica.
Si CA < 0 : Indica que la minoría de datos se encuentra en la parte izquierda de la media, en este caso se dice que la distribución es asimétrica negativa
Si CA = 0 : La distribución es simétrica
Si CA > 0 : Indica que la minoría de datos se encuentra en la parte derecha de la media, en este caso se dice que la distribución es asimétrica positiva.
Si lo que queremos es ver la forma en el sentido vertical, esto se calcula a través de un coeficiente que se conoce como Curtosis.
Curtosis K
La curtosis es una medida de forma que nos indica como de puntiaguda o de achatada está una curva o distribución.
$K=\frac{\sum\limits_{i=1}^n f_i \cdot (x_i – \overline{x})^4}{N \sigma^4 }$
Siendo $\overline{x}$ la media y $\sigma$ la desviación típica.
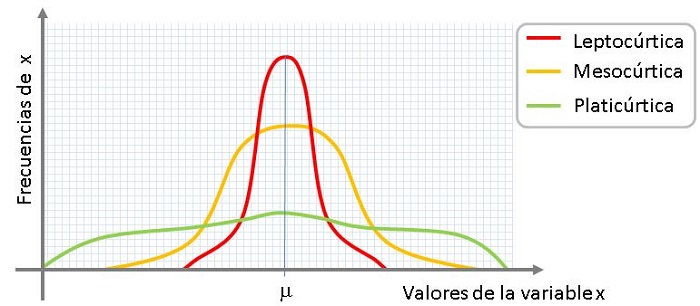
S K < 3: La distribución es achatada (Platicúrtica)
Si K = 3 a esta distribución se le llama Mesocúrtica
Si K > 3 : La distribución es «puntiaguda» (Leptocúrtica)
Una vez repasadas las medidas de forma más importates, adentrémonos en lo que más importa a la hora de elegir un fondo, su rentabilidad.
Rentabilidad
Se calcula aplicando la siguiente formula:
$Rentabilidad =\frac{(\text{Valor actual de la inversión -Valor inicial invertido) + Dividendos o Intereses }}{\text{Valor inicial invertido}} \cdot 100$
Veamos un ejemplo de cálculo de la rentabilidad de un fondo de inversión en una semana:
Suponiendo que en este caso el fondo no ha pagado dividendos, la rentabilidad a siete días de este fondo ha sido:
| día | valor liquidativo del fondo |
| día 1 | 10,01 |
| día 2 | 10,151 |
| día 3 | 10.312 |
| día 4 | 10,314 |
| día 5 | 10,401 |
| día 6 | 10,406 |
| día 7 | 10,500 |
Rentabilidad=$\frac{10,500-10,01}{10,01}\cdot 100=4,895 \% $
Sin embargo en la práctica, la mejor forma de calcular de la rentabilidad es ir calculando las rentabilidades intradía y sumarlas.
| Número de día | Valor liquidativo del fondo | Rentabilidad intra día | Valor liquidativo ficticio inicial |
| día 1 | 10,01 | 100 | |
| día 2 | 10,151 | $\frac{10,151}{10,01}-1=0,1408591$ | $100 + \frac{10,151}{10.01}-1 =100,01408591$ |
| día 3 | 10.312 | $\frac{10,312}{10,151}-1=0,01586051$ | $100,01408591+0,01586051= 100,029946$ |
| día 4 | 10,314 | $\frac{10,314}{10,312}-1=0,00019395$ | 100.03014 |
| día 5 | 10,401 | 0.00843514 | 100.038576 |
| día 6 | 10,406 | 0.00048072 | 100.039056 |
| día 7 | 10,500 | 0.00903325 | 100.048089 |
Por tanto la rentabilidad en una semana ha sido del 4,8%
Este método de ir calculando las rentabilidades intradía es mejor porque vamos teniendo en cuenta lo que pasa cada día, mientras que con el primer método solo nos fijábamos en lo que pasaba el primer y el séptimo día.
Lo habitual suele ser coger datos anualizados, si por ejemplo tengo datos de 6 meses y anualizo esa rentabilidad, es como «emular»«extrapolar» esos datos a cómo sería si en lugar de tener 6 meses hubiese tenido un año. Lo mismo se puede hacer con tres años, se puede anualizar que sería emular eso, pero a un año.
Lo que hemos calculado en el ejemplo anterior es lo que se llama la rentabilidad simple.
La rentabilidad anualizada indica el beneficio porcentual si el plazo de la inversión hubiese sido de un año.
La principal ventaja de la rentabilidad anualizada es que nos permite ver mejor la rentabilidad del fondo. Conocer que hemos ganado un 210 % en 10 años nos puede parecer bastante, pero es difícil discernir si es mucho o poco. Sin embargo, si nos dicen que la rentabilidad anual/anualizada es del 12 %, esto nos lo deja mucho más claro. Además, es la única forma de poder comprar la rentabilidad de un fondo del que conocemos cinco años de vida con la de otro del que conocemos quince. La forma de verlo claro es anualizando sus rentabilidades y comparándolas.
¿Preferimos ganar un 150 % en 25 años o ganar un 250 % en 30 años? En el primer caso, la rentabilidad anualizada es del 3,73% y en el segundo del 4,26%.
La fórmula de la rentabilidad anualizada es
Sea $R$ la rentabilidad simple o rentabilidad cuya fórmula ya hemos visto.
Sea $ndias$ la diferencia de días entre el valor inicial de la inversión y el valor actual de la misma.
$Rentabilidad Anualizada = ((\frac{R}{100}+1)^{\frac{365}{ndias}} -1 ) \cdot 100$
En el ejemplo anterior la rentabilida anualizada seria $((\frac{4,8}{100}+1)^{\frac{365}{7}} -1 ) \cdot 100$

Antes de elegir un fondo de inversión, lo normal es mirar la rentabilidad que ha tenido el fondo durante el último año -la rentabilidad simple del fondo a un año y su rentabilidad anualizada coinciden- y a continuacion la que ha tenido en los últimos años, claro, queremos ver si el fondo ha ganado dinero (rentabilidad positiva). Otro dato a tener en cuenta antes de elegir un fondo de inversión es su volatilidad, la desviación típica que ya hemos visto.
La volatilidad es lo que varía la rentabilidad de un activo respecto a su media en un periodo de tiempo determinado, cómo de volátiles son sus precios. Mucha gente lo ve como una medida de riesgo. Como inversores debemos tener en cuenta el nivel de riesgo que estamos dispuestos a asumir.
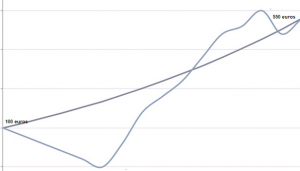
En esta gráfica se puede ver la rentabilidad de dos fondos de inversión, ambos han tenido la misma rentabilidad, pero uno ha ido creciendo de forma más o menos continua y el otro ha ido teniendo altibajos, siendo más volatil.
El fondo que nos gusta naturalmente es el que no ha tenido «sustos».
Podemos entender el riesgo como el nivel de incertidumbre sobre el resultado final.
Covarianza $\sigma_{xy}$
La vamos a estudiar porque nos va a servir para calcular el estadístico llamado Correlación.
La covarianza es la variable estadística que refleja en qué cuantía dos variables varían de forma conjunta (respecto a sus medias), refleja si existe relación entre dos variables en principio independientes.
La forma de calcularla es
$\sigma_{xy}= \frac{\sum\limits_{i=1}^n (x_i – \overline{x} )\cdot (y_i – \overline{y} )}{N}$
La covarianza es un dato muy bueno, pero tiene dos problemas
- No está acotada: En principio pensamos que cuanto más grande sea es mejor, pero a la vista de un resultado no sabemos cuanto es de grande porque no conocemos la cota superior.
- Arrastra las unidades de las dos variables x e y: Si estuviésemos estudiando la edad y el peso, la covarianza estaría expresada en años x kg, pero si quisiésemos estudiar la edad y la talla, la covarianza vendría expresada en años x cm. Evidentemente el valor numérico no es comparable cuando las unidades son tan diferentes.
Así que tendremos que hacerle una pequeña «transformación» para que este dato sea manejable (esta transformación será la correlación).
El signo que tiene la covarianza tiene gran interés en estadística.
Si tenemos una nube de puntos de la que queremos calcular la covarianza, lo que vemos observando la fórmula es que
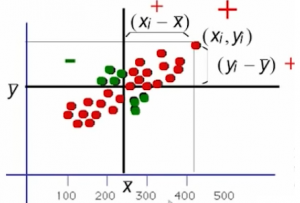
Los puntos en rojo van a aportar a la fórmula valores positivos, veamos por ejemplo los de $x_i$ e $ y_i$ positivos. Cada $x_i$ es mayor que su media y cada $y_i$ mayor que la suya, por tanto
$(x_i – \overline{x} )\cdot (y_i – \overline{y} )$ es un valor positivo.
Cuando los $x_i$ e $ y_i$ son negativos, como menos por menos es más, esos puntos también van a aportar valores positivos a la fórmula. Los puntos pintados en verde aportan valores negativos y como hay más puntos rojos que verdes al final la covarianza saldrá positiva.
A medida que aumenta la x aumenta la y, por tanto cuando la covarianza tiene un valor positivo, nos está indicando una relación directa entre las variables.
Mas concretamente:
$\sigma_{xy}$ es mayor que cero cuando “X” sube e “Y” sube. Hay una relación positiva.
$\sigma_{xy}$ es menor que cero cuando “X” sube e “Y” baja. Hay una relación negativa.
$\sigma_{xy}$ es igual que cero cuando no hay relación existente entre las variables “X” e “Y”.
Correlación r (coeficiente de correlación lineal de Pearson)
La correlación estadística nos indica si dos variables están relacionadas o no, relacionadas en el sentido de que un cambio en una implica un cambio en la otra. Se representa por la letra r y varía entre $-1\le r \le 1$
La fórmula de la Correlación es
$r = \frac{\sigma_{xy}}{\sigma_x \sigma_y} $
es decir, la covarianza de x e y partido por la deviación típica de x por la desviación típica de y. Con ello lo que conseguimos es «librarnos» de las unidades ya que la desviación típica tiene las unidades de la x por las unidades de la y, mientras que la desviación típica de la x, las unidades de la x y la desviación típica de y, las unidades de la y. Se anulan entre ellas y conseguimos un valor adimensional.
En el caso de los fondos de inversión, estas dos variables son, una el fondo y otra un índice de referencia o benchmark contra el que queremos comparar el fondo (por eljemplo el ibex 35 que es el principal índice de referencia de la bolsa española)
Ambas variables (fondo y benchmark) pueden estar correlacionadas de forma positiva o de forma negativa.
La correlación es positiva si sus rentabilidades se mueven en la misma dirección, arriba o abajo pero de la misma forma en ambas variables.
La correlación es negativa si cuando la rentabilidad de una sube, ello implica que la rentabilidad del otro baja.
Una correlación de valor 1 significa que la correlación es perfecta, se mueven igual.
¡Ojo!, un valor 0 o próximo a 0 de la correlación no quiere decir que dos variables son independintes. Lo contrario si es cierto, si son independientes la correlación es 0, pero pueden ser dependientes pero la relación no ser lineal y la correlación podría ser 0.
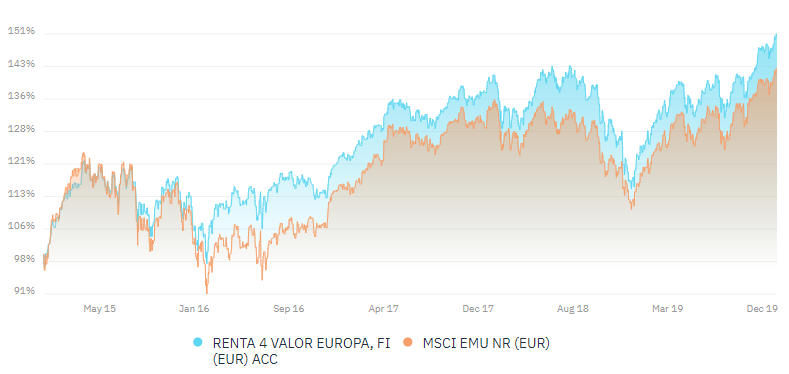
Veamos un ejemplo de correlación de valor 0,96 entre un fondo y un índice. Como podemos ver, prácticamente se mueven igual.
Vemos ahora un ejemplo de correlación entre un fondo y su indice de referencia con valor -0,19. Es una correlación negativa porque se mueven en direcciones opuestas.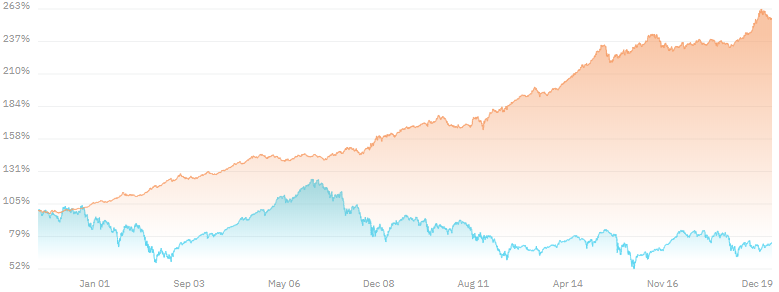
Máximo Drawdown
El máximo drawdown se define como la máxima caída experimentada por un activo/fondo en el periodo comprendido desde que se registra un máximo, hasta que vuelve a ser superado. A las caidas las denominados en general drawdowns.
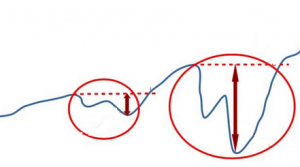
Es una forma de medir el riesgo de una inversión. A mayor drawdown, más dificil es recuperarnos, parece una perogrullada pero es así, a mayor pérdida, más complicado es volver al momento anterior. Veamosló con un ejemplo:
Si tenemos 10.000 euros y sufrimos un drawdown del 20%, la inversión se nos queda en 8000 euros. Para volver a quedarnos como estábamos, tenemos que generar un beneficio del 25% ya que 1,25*8000=10.000 . Una pérdida del 20% nos obliga a tener un beneficio del 25% para quedarnos como en el punto de partida.
Hasta este punto podríamos decir que hemos visto los estadísticos más importantes que se suelen mirar a la hora de elegir un fondo de inversión, Realmente y aunque no forma parte del objetivo de este tema, generalmente lo que se suele mirar para decidir qué fondo de inversión elegir suele ser (aunque sobre esto hay muchas opiniones):
1.- Primero miramos en qué queremos invertir, por ejemplo en robótica, cartón, oro, etc (es lo que se suele llamar el «asset allocation») para a continuación buscar fondos que inviertan en ello.
2.- Miramos que podamos pagar la aportación inicial mínima al fondo, así como las comisiones de este (comisión de gestión, depósito, reembolso, etc). Elijo la clase del fondo que más se ajuste a lo que queremos.
3.- La categoría (tipo de activo y zona geográfica en la que invierte el fondo) «nos da lo mismo».
4.- Rentabilidad anualizada, volatilidad, sharpe ratio y máximo drawdown del fondo.
El resto de estadísticos se miran menos, pero vamos a ver algunos de ellos:
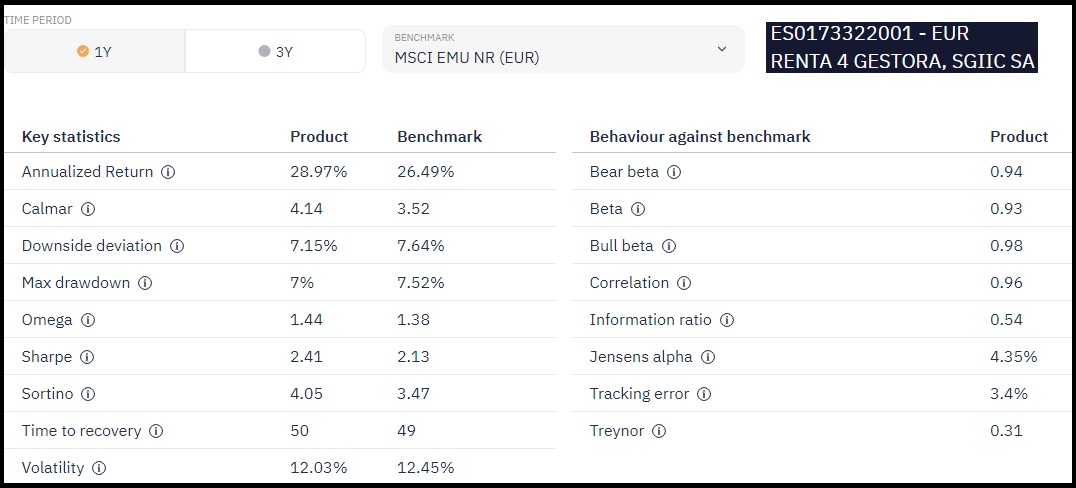
Beta $\beta$
La Beta de un fondo, es una medida de sensibilidad que nos indica la variación relativa de volatilidad que sufre dicho fondo en relación a un índice de referencia, es decir, es una medida que nos indica cómo le afecta al fondo el comportamiento del índice contra el que está referenciado.
Se utiliza sobre todo en el caso de fondos que invierten en renta variable.
El índice de referencia normalmente (aunque no tiene por qué) es el índice bursátil del mercado en el que invierte dicho fondo, como por ejemplo el Ibex35 para los fondos que invierten en este mercado, o el S&P 500 para el caso de la bolsa de de Nueva York.
Su fórmula es
$\beta = Correlacion \cdot \frac{\sigma_f}{\sigma_i}$
$\sigma_f$: Volatilidad del fondo anualizada
$\sigma_i$:Volatilidad del índice anulaizada
La beta puede ser positiva o negativa, si es positiva eso quiere decir que si el índice sube mi acción sube y si el índice baja mi acción baja. Si es negativa quiere decir que si el índice sube mi acción baja y viceversa.
Pero además puede ser mayor que 1 o menor que 1.
$\beta >1$ significa que si el índice sube un 1%, mi acción sube más de un 1 y si el índice baja un 1, mi acción baja más de un 1.
$\beta<1$ significa que si el índice sube 1 mi acción sube menos y si el índice baja un 1 mi acción baja menos de un 1%.
| Beta | Riesgo del índice | Valor de ejemplo | Interpretación |
| < 1 | Le afecta poco el comportamiento del índice | 0,5 | Lo que afecte al índice le afecta la mitad al fondo |
| = 1 | Igual riesgo | 1 | Si algo de mercado le afecta al índice, le afecta al fondo por igual |
| > 1 | Lo que le afecte al índice le afecta en mayor medida al fondo | 1,4 | Lo que afecte al índice le afecta al fondo en un 40% más |
Es decir si un fondo tiene un beta 1,15 respecto a su índice de referencia, eso significa que su volatilidad se va a mover un 15% más de lo que lo haga la de dicho índice.
Los tres siguiente ratios estadísticos nos indican si el fondo -o el gestor- lo ha estado haciendo bien o si lo ha estado haciedo mal usando como criterio la rentabilidad que le ha sacado al fondo en función del riesgo asumido.
Ratio de Sharpe.
El Ratio de Sharpe recibe su nobre de William Sharpe y relaciona la rentabilidad que ha obtenido un fondo de inversión con la volatilidad que ha sufrido, es decir nos ayuda a entender cómo ha conseguido la rentabilidad.
Su fórmula es:
$Sharpe Ratio=\frac{\text{Rentabilidad del fondo – Rentabilida del activo libre de riesgo }}{\text{Volatilidad del fondo}}$
El Sharpe Ratio o Ratio de Sharpe no tiene unidades ya que la rentabilidad se mide en porcentajes % y la volatilidad también por estar basada en porcentajes.
Se considera un activo sin riesgo o libre de riesgo a la deuda pública a corto plazo emitida por los países más desarrollados, como por ejemplo EEUU, la Unión Europea, etc. cuyo riesgo de impago por quiebra prácticamente no existe pues son muy solventes. Estos activos aseguran una rentabilidad conocida de antemano que no sufre variaciones (volatilidad). como inversores debemos pretender tener más rentabilidad que los activos libres de riesgo. En el banco para el que trabajo se utiliza para los cálculos como activo libre de riesgo el índice EONIA.
Observar que para que tenga sentido el dato del Ratio de Sharpe, la rentabilidad del fondo analizado debe ser mayor que la del activo libre de riesgo, o lo que es lo mismo, que el Ratio de Sharpe no tenga signo negativo, porque si esto fuese así nos convendría invertir en el activo libre de riesgo en lugar de en el fondo.
Cuanto mayor sea el Ratio de Sharpe, mejor será la rentabilidad que ha obtenido el fondo en relación a la volatilidad que ha tenido.
El Ratio de Sharpe nos sierve para elegir entre un fondo u otro, el valor del Sharpe Ratio de un fondo no sirve de nada si no lo comparamos contra algo, pero ojo, solo tiene sentido si ambos fondos pertenecen a la misma categoría (activo y zona), por ejemplo renta variable de la zona europa, por decir uno.
| Fondo A | Fondo B | |
| Rentabilidad a un año | 17% | 19% |
| Volatilidad a un año | 16% | 23% |
| Sharpe Ratio | (17-2)/16=0,93 | (19-2)/23=0,72 |
Nota: En este ejemplo hemos supuesto una rentabilidad del 2% del activo libre de riesgo.
El fondo A ha obtenido algo menos de rentabilidad que el fondo B, pero su ratio de Sharpe es bastante mejor. En mi caso concreto, yo dormiría mejor eligiendo el fondo A.
Lo que realmente nos está diciendo el Ratio de Sharpe es: Por cada unidad de riesgo añadida -para el fondo A, si la volatilidad es 17% en lugar de 16%- ¿qué rentabilidad me aporta de más?, la respuesta es 0,93 unidades.
Los sharpe ratios que tenemos que buscar son valores altos y en la medida de lo posibles mayores al valor 1. Como curiosidad, decir que los sharpe ratio de la mayoría de índices son menores que 1 y los fondos con más estrellas de valoración tienen un sharpe ratio mayor que 1.
Treynor Ratio
¿Dónde va Vicente? dónde va la gente.
Esta es la principal premisa en la que se basa la bolsa, San Vicente es el «patrón» de la bolsa. La Bolsa se basa en San Vicente. Si la gente compra yo suelo comprar y si la gente vende yo suelo vender. La Bolsa va subiendo y bajando porque todo el mundo hace lo mismo a la vez. Cuando esto pasa, entonces el valor de mi acción o fondo será parecido a la evolución conjunta del índice de la Bolsa.
El riesgo de una acción lo podríamos dividir entre:
- El riesgo sistemático: Es el riesgo de «San Vicente», el que no puedo quitar porque todo el mundo va con San Vicente.
- El riesgo específico: Este es el riesgo normal.
A todo el riesgo (sistemático + específico) es a lo que se le llama desviación estándar o volatilidad $\sigma$ .Con la Treynor ratio solo tendremos en cuenta el riesgo sistemático, es igual que el Sharpe Ratio pero solo teniendo en cuenta el riesgo sistemático, es decir, mediremos si le gestor lo está haciendo bien o mal gestionando el riesgo de «San Vicente».
Su fórmula es igual a la de Sharpe Ratio pero teniendo en cuenta la volatilidad sistemática.
$Treynor Ratio=\frac{\text{Rentabilidad del fondo – Rentabilida del activo libre de riesgo }}{\beta}$
La $\beta$ -que ya hemos visto- me dice cuanto se mueve mi acción por cada unidad de rentabilidad que se mueve el índice. Es el riesgo o volatilidad sistemática del mercado.
Alpha de Jensen $\alpha$
Este estadístico mide la diferencia entre la rentabilidad real y la rentabilidad esperada, dado el riesgo asumido con respecto a un índice. Se define como aquella parte de la rentabilidad de la inversión que es independiente del merdado. En caso que sea positivo el Alpha, quiere decir que nuestra inversión ha obtenido una mejor relación rentabilidad-riesgo que el índice, en otras palabras, mide la habilidad del gestor del fondo en obtener una rentabilidad superior a la del índice contra el que se referencia.
$Alpha = R_f \text{ }- ( \beta \cdot R_i)$
$R_f$: Rentabilidad del fondo para todo el periodo anualizada
$R_i$: Rentabilidad del índice para todo el periodo anualizada
En la fórmula aparece la $\beta$ y por tanto se basa en el riesgo sistemático.
Podemos verlo como la rentabilidad real – la rentabilidad teórica.

Mide la rentabilidad que un gestor tiene en un fondo de inversión, demostrando mejor habilidad cuanto mayor y positiva sea respecto a sus competidores.
$\alpha > 0$: Es la opción que todo gestor de fondos quiere. Si consigue un alpha por encima de 0, y además bate a la media de otros gestores de fondos, el gestor está aportando valor añadido al logar batir al mercado. Es decir, queremos Alphas de Jensen positivas y cuanto más altas mejor.
$\alpha = 0$: El gestor está replicando la rentabilidad del mercado.
$\alpha < 0$: El gestor se está durmiendo en los laureles.
Supongamos dos gestores de fondos
Gestor1 gestiona un fondo que ha tenido una rentabilidad anual del 5%, Beta=0’6 y Alpha de Jensen=3’5
Gestor2 gestiona un fondo que ha tenido una rentabilidad anual del 8%, Beta=1’6 y Alpha de Jensen=0’25
Viendo el Alpha de Jensen comprendemos que Gestor1 es mucho mejor gestor a pesar de haber conseguido menor rentabilidad en su fondo, ya que lo están haciendo asumiendo un menor riesgo medido por la beta que es del 0’6 frente al 1’6 de Gestor2.