Adam Smith no tenía razón.
Adam Smith en su obra «La riqueza de las naciones (The Wealth of Nations)», decía que «el interés propio de cada individuo conduce al bienestar general».
Veamos en qué consiste el dilema del prisionero.
Dos delincuentes son detenidos y encerrados en la cárcel en celdas distintas de forma que no puedan comunicarse entre ellos. La policía quiere acusarles del atraco de un banco, pero no tiene pruebas y sólo puede culparles de un delito menor que conlleva 6 meses de cárcel, de forma que a cada uno de ellos le propone lo siguiente -y ambos saben que se lo va a proponer también al otro.
Si confiesa que ambos fueron los atracadores, quedaras libre y su compañero será condenado a 10 años de cárcel.
Si su compañero también confiesa, ambos serán condenados a 6 años de cárcel.
Si ninguno de ellos confiesa, ambos serán condenados a 6 meses de cárcel.
Si su compañero confiesa y él no, su compañero quedará libre y él será condenado a 10 años de cárcel.
| Sospechoso B lo niega | Sospechos B confiesa | |
| Sospechoso A lo niega | Ambos son condenados a 6 meses | A es condenado a 10 años y B queda libre |
| Sospechoso A confiesa | A queda libre y B es condenado a 10 años | Ambos son condenados a 6 años |
Hay un conflicto entre el interes común y el interés propio. Por un lado lo mejor para ambos es callar, pero ¿y si el otro habla y pasas 10 años en la carcel aparte de quedarte con cara de tonto?.
Como ninguno sabe lo que va a hacer el otro preso, cada uno de ellos analiza las posibles opciones quedándose con la mejor para sus intereses:
El otro preso lo niega, entonces lo mejor es delatarle y quedar libre.
El otro preso confiesa, entonces lo mejor es delatarle y solo pasar 6 años.
Parece que lo mejor es delatar.
A este resultado es a lo que se conoce como un equilibrio de Nash -el matemático de la película «Una mente maravillosa». Este dilema se le atribuye a Tucker, profesor de Nash.
En un equilibrio de Nash cada actor maximiza sus ganancias teniendo en cuenta las posibles estrategias de los otros. Como consecuenca de ello, ningún actor puede elegir otra estrategia que le haga mejorar.
Un equilibrio de Nash no implica que se logre el mejor resultado conjunto para todos los actores del juego, sino solo el mejor resultado para cada uno de ellos considerados individualmente.
Este dilema se da en múltiples ejemplos como en carreras ciclistas a la hora de decidir si esforzarse o no, en los trabajos en equipo, etc y como hemos visto en él, está un poco reñido con lo que decía Adam Smith.
El dilema del prisionero es posiblemente el juego más utilizado en la teoría de juegos.
El conocido «juego del gallina» tiene varias versiones, una de ellas consiste en dos jovenes que se dirigen con sus coches uno contra otro a toda velocicad -lo hemos visto en algunas películas. El primero que se desvía pierde y el otro gana. Si ambos se desvían a la vez antes de chocar, empatan y si no lo hace ninguno de los dos, colisionan posiblemente muriendo ambos. Si llamamos X e Y a los dos jóvenes, si X gira el volante e Y no, el resultado es 20 puntos para X y 40 para Y. Si Y gira y X no, la puntuación es al revés. Si ambos mueven el volante, ambos reciben 30 puntos, pero si ninguno de los dos se desvía la «ganancia» es de 10 puntos para cada uno. Igual que en el dilema del prisionero esta situación, pero en otros escenarios, se da con mucha frecuencia en la vida y al igual que este, también se da el hecho de que, si un individuo persigue sólo maximizar sus beneficios personales, no lo consigue.
Teoría de Juegos
No debemos confundir la Teoría de Juegos con la Estadística, no son lo mismo, conceptos como probabilidad, etc, los utilzamos en el análisis de juegos de azar o para tomar decisiones ante situaciones aleatorias, mientras que la teoría de juegos estudia el comportamiento estratégico de los jugadores. En filosofía, economía, sociología, política, informática, biología, en el campo militar -en la guerra fría se utilizó mucho, el que ambas potencias siguieran aumentando el gasto en armamento es un ejemplo claro del dilema del prisionero-, etc, el resultado final depende de las decisiones que tomen otras personas -o jugadores- y que les afectan.
La teoría de juegos es una rama de las matemáticas que estudia el comportamiento de jugadores que interactúan y toman decisiones dentro de unas reglas claramente definidas -juegos- y que tratan de maximizar su beneficio sabiendo que los otros jugadores toman decisiones racionales (esto es importante).
En teoría de juegos, la palabra juego se refiere a un conflicto que afecta a un determinado número de personas -jugadores.
La teoría de juegos analiza estos -juegos- entendidos como situaciones en las que aparece un conflicto de intereses, existen una reglas que cumplen los jugadores y el objetivo es encontrar la opción óptima para conseguir el resultado deseado bajo las circunstancias dadas.
En estos juegos a veces la información es incompleta y los jugadores no conocen todas las características del juego.
Todo juego tiene unas reglas y los posibles resultados que pueden darse cuando la partida termina -recompensas en función de la estrategia seguida.
Las jugadas de los distintos jugadores pueden ser simultáneas o alternativas.
¿Y qué ganamos tras el juego?, pues dependiendo del juego a veces se declara un ganador o un perdedor -ajedrez-, en otros las ganancias dependen de lo que haya apostado el jugador.
Dentro de los juegos, se dice que se ha llegado a un equilibrio si ninguno de los jugadores puede mejorar su situación si los otros jugadores no modifican sus estrategias.
Los juegos se pueden representar en
a) FORMA NORMAL:
Es el caso en el que los jugadores actúan simultáneamente y sin conocer la elección que toma el otro.
Se representa con una matriz con los jugadores, acciones y dentro de la matriz las recompensas.
| Opción 1 (jugador B) | Opción2 (jugador B) | |
| Opción 1 (jugador A) | (A1,B1) | (A2,B2) |
| Opción 2 (jugador A) | (A3,B3) | (A4,B4) |
$A_i , B_i $ es el resultado de cada jugador según la opción elegida.
b) FORMA EXTENDIDA
Se trata de juegos con algún orden que se debe considerar.
Los juegos se representan como árboles en los que cada nodo representa un punto en el que el jugador toma decisiones.
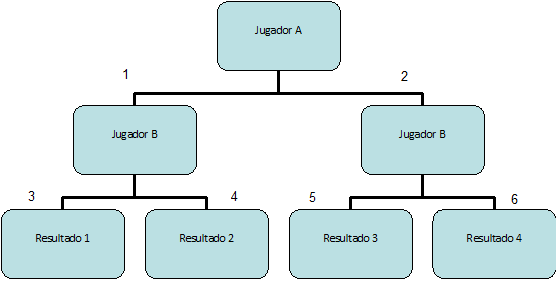
Este gráfico sería la forma extendida de un juego con dos jugadores A y B. El jugador A mueve primero y puede elegir entre los movimientos 1 o 2. El jugador B puede elegir los movimientos en función de lo elegido A. Al final se llega a cuatro posibles resultados.
Cuando ante un problema hay un único decisor, eso es un problema de optimización, pero cuando hay varios, eso es teoría de juegos.

