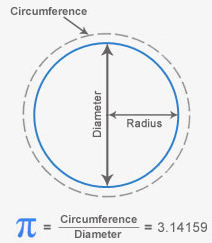
Sabemos que $\pi$ es irracional.
Continuamente hay noticias acerca de que se ha conseguido calcular «n» trillones de decimales del número $\pi$, lo cual no tiene gran utilidad, yo lo veo como algo así a cuando vemos una montaña a lo lejos y queremos llegar a ella para conocer lo que hay más allá.
El otro día leyendo un artículo sobre cuantos decimales del número $\pi$ utilizan en la NASA, explicaban que los ingenieros utilizan 3.141592653589793 y que con ello era suficiente.
Yo supongo -aunque esto ya es imaginación mía- que algo tendrá que ver el que, en sistemas operativos de 64 bits, 16 sea el máximo número de dígitos que puede tener la mantisa de un número real.
Pero en el día a día, ¿con cuántos decimales -a mi entender- debería sentirse cómodo un físico o ingeniero en sus cálculos «terrestres»?
Sabemos que la longitud del perímetro de la circunferencia es $ l=2 \cdot \pi \cdot r$
El radio de la tierra en su punto de mayor longitud -en el ecuador- es de 6.378km, cojámosle como radio de la tierra para este «experimento» -aunque también podríamos coger un radio que sea la media de diferentes mediciones de distancias desde distintos puntos del planeta. En nuetro caso obtenemos que la longitud de esta es algo menor a $2 \cdot \pi \cdot 6.378=12.756 \cdot \pi $ km
Si tomamos $\pi =3,14$ la longitud de la circunferencia es de 40.053,84 km.
Si tomaos $\pi=3,14159$ la longitud de la circunferencia es de 40.074,122 km.
Si tomamos $\pi=3,1415926$ la longitud de la circunferencia es de 40074,155 km.
Llegados a este punto, si tomamos $\pi=3.14159265358979$, es decir, tomamos los 16 decimáles que como máximo mi ordenador va a poder utilizar, resulta que la longitud del perimetro de la circunferencia terrestre saldría ya también 40074,155 km (el error de cálculo está por debajo de 1m)
La conclusión que obtengo es que, salvo para casos «estelares» como los necesitados en la NASA, con siete decimales obtenemos muchísima precisión y no deberíamos necesitar ninguno más.