El universo en el que vivimos tiene sentido en tres dimensiones -en cuatro, contando la dimensión temporal. El cerebro humano es incapaz de ver en más de tres dimensiones, solo somos capaces de ver en un sistema de coordenadas en el que los ejes siguen tres direcciones diferentes que forman ángulos rectos entre sí. Si queremos acceder a más dimensiones, únicamente podemos hacerlo mediante las matemáticas.
Las matemáticas nos permiten trabajar con espacios de cualquier número de dimensiones, así podemos representar puntos del espacio tetradimensional mediante grupos de cuatro números (x, y, z, t) y en general puntos de un espacio n-dimensional mediante puntos de la forma $(x_1,x_2,…,x_n)$
La realidad podría perfectamente tener más dimensiones de las que nosotros somos capaces de ver, de hecho, hay teorías como la Teoría de Cuerdas que indica que puede haber once dimensiones (10 dimensiones + 1 temporal).
Imaginemos que somos seres vivos de dos dimensiones, es decir, vemos los conceptos de izquierda y derecha, delante y detrás, pero no vemos el arriba y abajo. Si nos pusiesen sobre el suelo rodeados de un círculo hecho con la cuerda de un zapato, no podríamos salir de él y ese sería para nosotros nuestro mundo, no se nos ocurriría saltar para salir.
¿Cómo veríamos una lata de Coca-Cola?, al ser un objeto de tres dimensiones, no podríamos verlo – aunque exista- únicamente podríamos ver la proyección del cubo sobre la superficie bidimensional en la que creemos vivir, es decir, veríamos un círculo plano sobre el suelo. Para nosotros la realidad sería plana.
Aplicando un razonamiento parecido, como nosotros vemos en tres dimensiones, ¿por qué no puede ser que lo que estemos viendo sea la proyección de objetos de cuatro dimensiones?.
En la práctica, como humanos, únicamente podemos ver en tres dimensiones, pero con las matemáticas ese «tres» puede ser «n».
No te fíes de lo que veas, sino de lo que te digan las matemáticas. Hace 2500 años, cuando a caballo únicamente se podían recorrer unos cuantos kilómetros en un día y todo se veía plano, era normal que la gente pensase que la tierra era plana, Pitágoras fue el primer griego en vislumbrar que la tierra era redonda, aunque naturalmente no lo veía, pero se lo decían las matemáticas.
¿Por qué la realidad espacial tiene que ser de tres dimensiones?, las matemáticas nos permiten ver más allá de lo que ven nuestros ojos y, de hecho, posiblemente la realidad espacial tenga más dimensiones de las que nosotros percibimos.
Vamos a centrarnos en intentar comprender un mundo de cuatro dimensiones y para ello vamos a ir poco a poco entendiéndolo de menos a más:
Una línea recta es algo unidimensional porque solo tiene longitud, no tiene ni anchura ni altura.
Una circunferencia es una curva formada por todos los puntos de un plano que se encuentran a la misma distancia -radio- de un punto al que llamamos centro y al igual que la línea recta, es unidimensional.
Una circunferencia incluye también su interior, es solo la «fina línea curva», si incluyese su interior a eso en matemáticas se le llama disco. Una circunferencia es un objeto unidimensional que puede colocarse en un objeto bidimensional como un plano. Un dibujo de una circunferencia sobre un folio de papel puede servirnos para visualizarlo mejor.
Una esfera está formada por todos los puntos situados a la misma distancia de un punto dado en un espacio tridimensional. Está formada únicamente por los puntos que «situados» su superficie, es decir, es una superficie curva -tiene dos dimensiones-, no está rellena, en matemáticas si estuviese rellena lo llamaríamos bola.
Las esferas de dimensiones más dimensiones se llaman hiperesferas, hemos dicho que la esfera tiene dos dimensiones así que la hiperesfera más sencilla es la 3-esfera, y es un objeto tridimensional inserto en un espacio tetradimensional.
Los seres humanos no podemos ver en cuatro dimensiones, pero podemos tratar de imaginarlo por analogía. Igual que una circunferencia es una línea curva y una esfera es una superficie curva, una 3-esfera es un volumen curvo.
Vamos a pararnos aquí y leer los tres últimos párrafos de nuevo si fuese necesario porque son necesarios para entender lo siguiente y casi terminar de «verlo»:
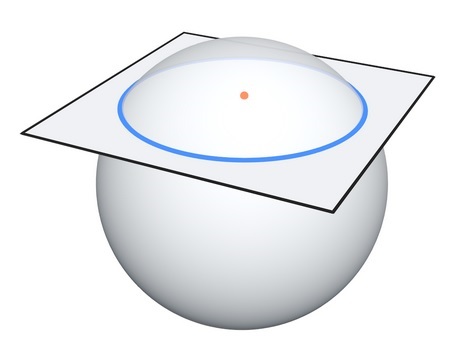
Supongamos que fuésemos seres bidimensionales que vivimos en un plano, solo veríamos puntos y líneas de diferente longitud. Si una esfera atravesase el plano en el que vivimos -o folio de papel si lo entendemos así mejor-, cuando la esfera en tres dimensiones toca inicialmente nuestro plano en dos dimensiones, veríamos un punto, que luego crece convirtiéndose en una circunferencia, que alcanza un diámetro máximo igual al diámetro de la esfera, antes de que la circunferencia se reduzca de nuevo hasta convertirse en un punto para luego desaparecer cuando la esfera termina de atravesar el plano.
Igualmente, si una 4-esfera atravesase nuestro espacio, la veríamos como un punto que se expandiría hasta convertirse en una esfera tridimensional para finalmente ir reduciendo su tamaño hasta desaparecer. La 4-esfera en sí no la veríamos.
Un ser tetradimensional tiene «poderes» en nuestro mundo. Como ejemplo, podría coger un guante de la mano derecha, darle la vuelta en la cuarta dimensión y volver a ponérselo en la mano izquierda como si fuese magia.
Imaginemos un guante bidimensional, que sería como una línea fina con la forma de la mano derecha. Podemos recortar una forma semejante en un papel, levantarla, darle la vuelta y volver a bajarla, con lo que habríamos cambiado su lateralidad para la mano. A un ser en dos dimensiones esto le dejaría fascinado, pero, para nosotros que tenemos una dimensión extra, el truco nos parece sencillo.
En una cuarta dimensión, una forma tridimensional podría rotarse hasta convertirse en su imagen especular.
Un ser de una cuarta dimensión, podría ver lo que tuviésemos guardado dentro de una caja de zapatos, mientras que para los humanos que solo percibimos tres dimensiones esto nos resulta algo imposible de entender. Este superpoder se lo da el percibir cuatro dimensiones.
Para entender esto bien, vamos a pensar en un insecto o un ser que solo perciba dos dimensiones y que viva sobre un plano, sobre su plano pondremos un hilo de coser en forma de rectángulo que represente nuestra caja de zapatos, y dentro del rectángulo pondremos una goma de borrar, aquí el ser bidimensional solo podría ver el exterior de este rectángulo, pero un ser que viva en tres dimensiones como nosotros, miraría por arriba y podría ver tanto el contorno -hilo- de la caja de zapatos, como el interior, incluso podría ir más lejos y coger -sacar- la goma de borrar de su interior. Esto al insecto que solo ve en dos dimensiones le parecería increíble -ver lo que hay dentro y encima poder cogerlo.
Pues entendiendo esto, podemos entender que un ser que perciba cuatro dimensiones pueda hacer lo mismo con nuestra caja de zapatos, es decir, poder ver su interior e incluso coger lo que hay dentro sin necesidad de abrirla.