Las Matemáticas son divertidas.
Las integrales múltiples $\iiiint_V \mu(t,u,v,w) \,dt\,du\,dv\,dw$ tienen sentido sobre todo con funciones de más de una variable independiente. ¿Para qué utilizamos las integrales múltiples?, en esta entrada veremos algunas aplicaciones de este tipo de integrales poniendo el énfasis en las dobles.
Continuar leyendo «¿Para qué sirven las Integrales Múltiples?»
Es uno de los considerados siete problemas de matemáticas del milenio y para los que el Instituto Clay de Matemáticas ha ofrecido un millón de dólares a quien lo resuelva, ¿en qué consiste?.
Las matemáticas están íntimamente unidas a las demostraciones, unas matemáticas sin demostración no serían matemáticas, las matemáticas van cogidas de la mano de estas, no se concibe una cosa sin la otra. Es lo que les da su principal característica: Rigor, robustez y confianza.
Siempre que demostramos algo seguimos los siguientes pasos: Primero, enunciamos unas hipótesis, que son una serie de condiciones previas que se sabe que son factibles, después enunciamos la tesis, que es el descubrimiento en sí (el resultado), y tras esto escribimos la demostración de la tesis, que son una serie de razonamientos que nos llevan desde la(s) hipótesis hasta la tesis a través de pasos que deben estar siempre bien justificados.
Hay muchos tipos de demostraciones. El pensamiento deductivo para hacer demostraciones se va adquiriendo poco a poco (como me gusta decir a mí, por sedimentación). El trabajo con demostraciones ayuda a desarrollar procesos como la abstracción, el análisis, la síntesis, la clasificación, la particularización, la comparación o la generalización. La demostración es la cumbre de la argumentación racional.
Vamos a ver algunos tipos de técnicas que solemos utilizar los matemáticos para demostrar cosas:
En esta entrada vamos a revisar conceptos de estadística y veremos como estos se aplican en el ámbito de los fondos de inversión. Con la estadística, obtenemos información a partir de los datos que tenemos y esto nos permite conocer si el fondo lo está haciendo bien, o si por el contrario lo está haciendo mal en comparación con otros fondos similares.
Cuando un cliente decide comprar un fondo de inversión, tiene que fijarse en varias cosas , entre ellas están el periodo de tiempo que tiene pensado mantener la inversión, el nivel de riesgo dispuesto a asumir, las comisiones que le van a cobrar en el fondo que finalmente elija (comisión de gestión, de suscripción, …), las rentabilidades que ha ido obteniendo el fondo hasta la fecha y varias cosas más entre las que se encuentra el objeto de esta entrada, los datos estadísticos del fondo o al menos algunos de ellos (los más importantes).
Vamos a empezar definiendo estos conceptos estadísticos empezando por alguno fácil que necesitaremos para comprender los demás.
Con las integrales nos suele pasar lo mismo que con las derivadas, aprendemos a integrar funciones, pero no sabemos realmente cual es la utilidad práctica de todo esto, lo cual hace que se estudien sin motivación.
Podemos convertir cualquier mensaje en un número, por ejemplo, asignándole un código de dos dígitos a cada letra y haciendo una cadena con esos números. La forma más sencilla sería sustituir las letras así: A = 01, B = 02, etc.
Esta sería una forma válida de encriptar un mensaje.
Continuar leyendo «Números primos y criptografía»
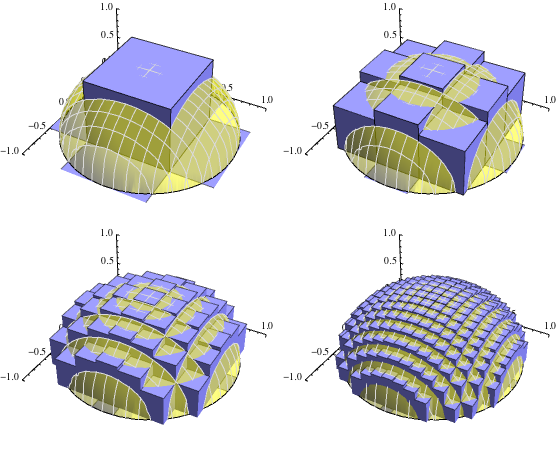
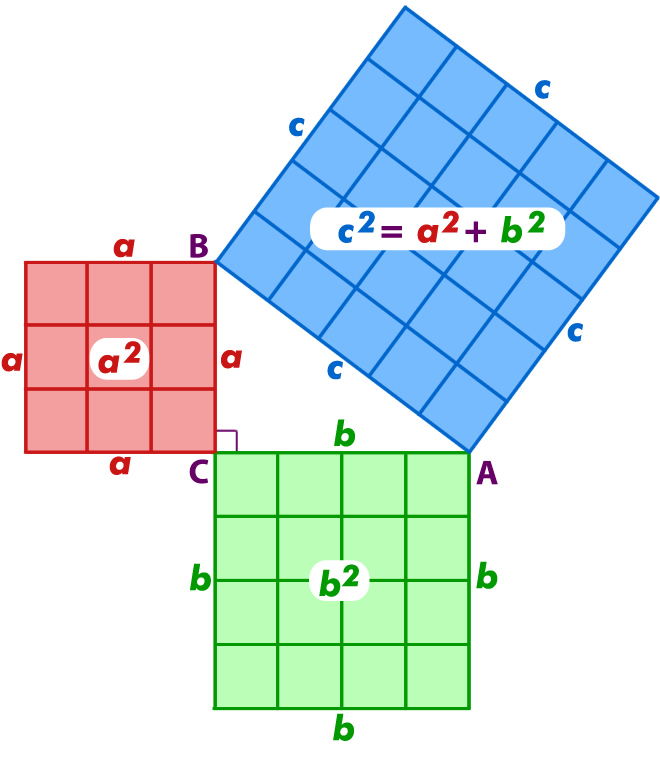
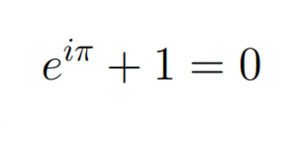En realidad, todos los números son conceptos humanos que modelan la realidad y que han ido apareciendo a medida que el hombre ha ido teniendo necesidades de ellos. Es muy bonita e interesante la histórica de como fueron apareciendo los distintos tipos de números, los naturales positivos, los naturales negativos, el cero, los racionales, los irracionales, los complejos… pero no es el objetivo de esta entrada.
Los números son realmente una invención humana para poder representar la realidad y poder contar, comerciar, etc.
Los números son una abstracción, lo que para nosotros es el símbolo 3 por ejemplo, en China utilizan otro símbolo.
Todos los números son muy interesantes, el tema de los números “no interesantes” lo zanjó el gran Martin Gardner diciendo que si hubiera números no interesantes, los podríamos ordenar en una lista y el primero de esa lista ya tendría una propiedad muy interesante.
En cualquier caso, es cierto que unos son más interesantes que otros, veamos unos cuantos.
La existencia del número π es conocido desde la antigüedad, pero el cálculo exacto del número no ha sido posible durante siglos.
Veamos tres de los más bellos métodos de calcular el valor del número π
Si hacemos esta pregunta a un determinado número de personas elegidas al azar probablemente nos responderán que son «el estudio de los números» o «la ciencia que estudia los números». Tremendo error que aún se sigue arrastrando, ya que esto era así hace 2500 años, pero no hoy.
He aquí un listado de elementos, frases, fórmulas matemáticas, etc, que todo mezclado da lugar a lo que podría llamarse una ensalada matemática, espero que lo disfrutes.
Continuar leyendo «Ensalada matemática (Σ, φ, ∫, ∉ ,≥ , ¬, ∞, …)»