He aquí un listado de elementos, frases, fórmulas matemáticas, etc, que todo mezclado da lugar a lo que podría llamarse una ensalada matemática, espero que lo disfrutes.
Pitagóricos: «Todo es número»
Galileo Galilei: «El universo está escrito en el lenguaje de las matemáticas»
Galileo Galilei: «Si comenzase de nuevo mis estudios, seguiría el consejo de Platón y comenzaría con las matemáticas»
Gauss: «Las matemáticas son la reina de las ciencias»
Arquímedes: «Dadme un punto de apoyo y moveré el mundo»
Newton: «If I have seen a Little further it is by standing on the shoulders of Giants»
Descartes: «Cogito ergo sum» Pienso luego existo
Pitagoras: «El principio es la mitad de todo»
Platón: «Los números gobiernan el mundo»
Texto que se encontraba escrito en la puerta de la ACADEMIA de Platón: «Nadie entre aquí que no sepa geometría».
Leonardo da Vinci: «Ninguna investigación humana puede ser llamada verdadera ciencia si no puede ser demostrada matemáticamente»
Introductio in analysin infinitorum (Leonhard Euler)
$$\text{Registro matemático: }\forall\exists\Rightarrow\land\sum_{n=1}^{\infty}a_n\int\frac{df}{dx}\lim_{x\to \infty}\not\in\supseteq\emptyset \text{…}$$
$$ \text{Problemas clásicos de Grecia}\begin{cases}\text{Cuadratura del círculo} \\ \text{Duplicación del cubo} \\ \text{Trisección del ángulo} \end{cases}$$
A demostrar se aprende demostrando. Reducción al absurdo, Inducción, Contraposición, Regresivo-Progresivo, …
Teorema isoperimétrico de Steiner: De todas las figuras planas con un perímetro dado, el círculo encierra el área máxima.
Teorema central del límite. Campana de Gauss.
Teorema fundamental de la aritmética
Teorema fundamental del álgebra
Teorema de Abel-Ruffini
Ley de los grandes números vs Regla de Laplace
Función de Weierstrass (continua y no derivable en ningún punto)
Si tenemos dos conjuntos de numeros, puede ocurrir que al mover un valor de un conjunto al otro, la media de los dos conjuntos aumente. Para que esto ocurra se deben cumplir dos condiciones: el número movido debe ser inferior a la media de su conjunto original y superior a la de su conjunto de destino.
| Ley de Benford | Constante de Kaprekar | Método de Montecarlo |
| Ruffini. Factorización de polinomios | Diagramas de Venn | Tangram |
| Tablero de Galton | Navaja de Ockham | Asno de Buridán |
| Divide y vencerás |
Esperanza matemática | Teoremas de Thales |
| Los Elementos (Euclides) |
Conjetura de Poincaré (Grigori Perelman) |
$$\frac{355}{113}$$ |
| Último teorema de Fermat (Wiles) | Hipótesis de Riemann (Función zeta de Riemann) | Apeirofobia |
| Lema de Sperner | Los siete puentes de Könisberg | Conjetura de Goldbach |
| Desigualdades de Young, Hölder y Minkowski | José Echegaray | Sucesión de Faray |
| Teoría de Galois | Regla de Cramer | |
| Teorema de Cantor | Identidad de Bézout | |
| Aporías de Zenón | Paradoja Sorites | |
| Conjetura de Goldbach | Espacio de Hilbert | La función tau de Ramanujan |
| Algoritmo de Euclides | Método del círculo de Hardy-Littlewood | Serie de Fourier |
| Numeración de Gödel | Función phi de Euler | Criba de Eratóstenes |
| Primos de Mersenne | Enteros de Gauss | |
| Lemniscata |
$$\sin^2(x)+\cos^2(x)=1$$
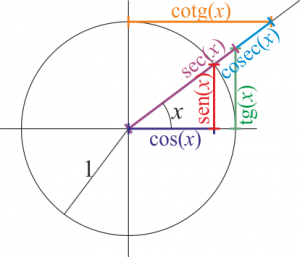 Fuente imagen: http://laplace.us.es/wiki/index.php/Tabla_de_f%C3%B3rmulas_de_trigonometr%C3%ADa
Fuente imagen: http://laplace.us.es/wiki/index.php/Tabla_de_f%C3%B3rmulas_de_trigonometr%C3%ADa
Números inconmensurables
3435 Número de Munchausen
2520 número perfecto. Se puede dividir de manera exacta por los números del 1 al 10
101 Primo Palindrómico
OMIRP: 73 es el 21º número primo. 21 al revés es 12. El 12º número primo es 37 y 37 al revés es 73
El 31 también es un OMIRP (primo)
142857 Número Cíclico
$$\text{Teorema de Bayes: } P(B/A)=\frac{P(B)}{P(A)}P(A/B)$$
$$\text{Fórmula de Euler Poliedros } C + V = A + 2$$
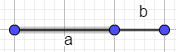
$$\textbf{Número aureo }\varphi=\frac{1+\sqrt{5}}{2} \text{ ; } \frac{a+b}{a}=\frac{a}{b} \text{ ; } \varphi =\frac{a}{b}$$
$$\textit{Fibonacci } 1, 1, 2, 3, 5, 8, 13, 21, …, x, y, … \text{ } \varphi\approx y-x$$
$$\text{Grandes problemas de la actualidad}\begin{cases}\text{P frente a NP}\\ \text{Conjetura de Hodge} \\ \text{Hipótesis de Riemann} \\ \text{Yang-Mills y el salto de masa} \\ \text{Las ecuaciones de Navier-Stokes} \\ \text{Conjetura de Birch y Swinnerton-Dyer} \end{cases}$$
¿Cuál es la diferencia entre hipótesis y conjetura?. El termino hipótesis tiene una connotación mucho más fuerte que el de conjetura, si algo es una hipótesis eso significa que aunque no se ha demostrado aún, se cree mucho en que en algún momento se demostrará, de hecho, se utilizará como hipótesis de trabajo para demostrar otras afirmaciones y en el momento en que esa hiptótesis pase a ser teorema, quedará demostrado de un plumazo todo lo que depende de ella. En cambio, una conjetura es simplemente una previsión de como un matemático cree que se comportará algo.
$$\text{Serie de Grandi : } 1 – 1 + 1 – 1 + 1 – 1 +1 – 1 + 1 – 1 + 1 – 1+1 – 1 + 1 – 1 + 1 – 1+ … $$
$$\pi=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}-\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}-\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}+…\text{Euler}$$
$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{11}-\frac{1}{13}+…\text{Leibniz}$$
$$\pi=\frac{2}{\sqrt{2}} \cdot \frac{2}{\sqrt{2+\sqrt{2}}} \cdot \frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}} \cdot …\text{Vieta}$$
$$ 1-2+3-4+…=\frac{1}{4}$$
$$e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}$$
$$e=\lim_{x\to \infty} (1+\frac{1}{f(x)})^{f(x)}$$
$$\lim_{n\to \infty} (1+\frac{1}{n})^n = e = \frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+… $$
$$\text{Un día vi una vaca vestida de uniforme } \int u \cdot dv=uv-\int v\cdot du$$
$$y=f(x); F(x,y)=0; y’=\frac{dy}{dx}=-\frac {\frac{\partial F}{\partial x}} {\frac{\partial F}{\partial xy}}=-\frac{F_x}{F_y}$$
$$\text{Euler } e^{ix}=\cos x + i\sin x$$
$$\text{igualando } x=\pi \text{ tenemos } e^{i\pi}=-1+i\cdot 0$$
$$ \mathbf{e^{i\pi}+1=0}$$
$$ 1 = 0,\overline{9} \text{ ; Demostrémoslo: } \frac{1}{3}=0’\overline{3} \Rightarrow 3\cdot \frac{1}{3}=0,\overline{9} \Rightarrow 1=0,\overline{9}$$
$$\text{Indeterminaciones}\begin{cases}
\frac{\infty}{\infty} \\
\frac{0}{0} \\ \frac{n}{0} \\ 0 \cdot \infty \\ \infty – \infty \\0^0 \\ \infty^0 \\ 1^\infty \end{cases}$$
¡Ojo!
$$\infty + \infty=\infty \text{ y } -\infty – \infty=-\infty$$
$\frac{0}{\infty}=0$
$\frac{\infty}{0}=\infty$
$0^0=1$
$0^{\infty}=0$
${\infty}^{\infty}=\infty$
$$\lim_{x\to \infty} (1+\frac{1}{x})^x = (1+\frac{1}{\infty})^\infty ={(1+0)}^\infty =1^\infty $$
indeterminación que en este caso concreto es e pues partimos de la definición de e.
Los símbolos que utilizamos para representar los números en la actulaidad y que son de origen indo-arábigos, fueron introducidos en occidente por el matemático Leonardo de Pisa , más conocido como «Fibonacci».
La línea horizontal que utilizamos para separa el numerador del denominador en una fracción también es de origen árabe y lo introdujo en occidente Leonardo de Pisa.

El símbolo «x» que se utiliza para la multiplicación se introdujo por la Cruz de San Andrés, más tarde Leibniz, empezó a utilizar el punto en lugar de la «x» para no confundirla con la variable X, También de Leibniz son los dos puntos «:» para designar la división.
Robert Recorde introdujo el símbolo de la igualdad «=» justificaba el uso de este símbolo diciendo que no hay dos cosas que puedan ser más iguales que dos rectas paralelas.
El símbolo infinito $\infty$ lo introdujo Wallis.
Euler introdujo los símbolos de los números $i, e$ y aunque no lo introdujo él, si que fue quien hizo popular el uso del símbolo $\pi$.
También introdujo Euler el símbolo $\sum$.
La notación y’ y f'(x) de las derivadas la introdujo Lagrange, mientras que la notación $\frac{dy}{dx}$ o $\frac{df}{dx}$ se las debemos a Leibnitz.La notación de las integrales la introdujo Leibnitz. La que utilizaba Newton era muy compleja.
La notación para la integral definida es de Fourier.
François Viète fue el primero en emplear letras para simbolizar las incógnitas y constantes en las ecuaciones algebraica.
Al principio, para indicar la raíz de un número se escribía «raíz de …» . Luego, para abreviar, se empezó a poner «r» y cuando el número era largo, el trazo horizontal de la «r» se alargaba hasta abarcar todas las cifras. Así surgió el símbolo actual de la raíz.
SEPARADOR DECIMAL: El primero en usar la coma para separar la parte entera de la decimal fue Giovanni Magini. Leibnitz le apoyó y propuso usar el punto como símbolo de multiplicación (en lugar del signo x, que se confunde con la incógnita X). En Inglaterra, sin embargo, en donde Leibnitz no era bienvenido por sus disputas con Newton, se siguió utilizando el símbolo x para la multiplicación y el punto para separar los decimales.
A Claude Elwood Shannon, matemático estadounidense, le debemos el término de bit usado tanto en informática (abreviatura de Binary digIT).
Los dos acontecimientos matemáticos que más repercusión han tenido en la prensa a nivel mundial han sido sin duda la demostración de Andrew Wiles del último teorema de Fermat y la de Grigori Perelman de la conjetura de Poincaré.
Todos los números son especiales porque si hubiese alguno que no fuese especial, sería el primero en no serlo y eso le convertiría en especial.
Este razonamiénto es similar al que daba Anselmo de Canterbury sobre la existencia de Dios: Si Dios es el Ser Más Perfecto y Dios es el ser más perfecto en la mente -en el mundo de las ideas-, Dios tiene que serlo también en la realiadad porque si no fuese así, habría otro ser superior en la mente y en la realidad, y eso no puede ser, ¿cómo puede ser concebible que el ser más grande en la mente no sea el ser más grande en la realidad?.
Kurt Gödel también justificó la existencia de Dios utilizando la lógica.
Los teoremas de incompletitud de Gödel, fueron para las matemáticas un jarro de agua fría, aa existencia de proposiciones ciertas, pero indemostrables dan mucho que pensar, como en el «Tío Petros y la conjetura de Goldbach»(A. Doxiadis, 1992) ¡a ver si esto que estoy tratando de probar resulta que no puede ser demostrado!.
Números Áleph: $\aleph$ es la primera letra del alfabeto hebreo y en matemáticas representa los distintos tipos de infinito que hay, así $\aleph_0$ representa el número de elementos de un conjunto infinito como el de los números $\mathbb{N}$. George Cantor demostró que existian diferentes tipos de infinitos, de hecho $\aleph_0$ representaría el conjunto de elementos infinitos más pequeño. El siguiente es $\aleph_1$, luego $\aleph_2$, etc.
Es muy conocida la siguiente conversación entre el matemático inglés G. H. Hardy y su ayudante, el matemático indio Ramanujan. Estando Ramanujan enfermo en el hospital, Hardy fue a visitarle y cuando llegó le dijo que el 1729 era el número de la matrícula del taxi que le había llevado y que un número bastante soso, a lo que Ramanujan que tenía una cabeza increíble para los números, le replicó casi inmediatamente: «¡No, Hardy! Es un número muy interesante. Es el menor número que se puede expresar como suma de dos cubos de dos maneras distintas». $9^3+10^3=1^3+12^3=1729$.
G. H. Hardy estaba «obsesionado» con probar la Hipótesis de Riemann -sigue sin estar probada-. Hardy era ateo y presumía de ello. En verano solía ir a visitar a su amigo el matemático Harald Bohr a Dinamarca, un año permaneció con él hasta el final de sus vacaciones de verano, por lo que tenía que volver sin falta a Inglaterra para comenzar con sus clases. Sólo había un pequeño barco en ese momento para volver y a veces el Mar del Norte puede estar bastante revuelto así que le preocupó la pequeña probabilidad que había de sufrir un naufragio. Cogió el pequeño barco, pero antes le mandó una postal a Bohr con el siguiente texto:
«He probado la Hipótesis de Riemann».
Los matemáticos de la época sabían que Hardy estaba trabajando en ello, así que pensó que Dios no le dejaría morir llevándose la gloria de haber probado la hipótesis y preferiría dejarle vivir y hacer el ridículo por haber mentido.
Cuando Carl Friedrich Gauss -seguramente el mejor matemático de todos los tiempos- tenía 10 años, como el profesor quería tener un poco de tranquilidad, mandó a sus alumnos sumar los cien primeros números naturales (1+2+3+…+100). Transcurridos unos pocos segundos Gauss levanto la mano y dijo tener la solución: los cien primeros números naturales sumaban 5.050.
El profesor se quedó estupefacto y le preguntó cómo lo había averiguado. Gauss se dio cuenta de que la suma del primer número con el último (1+100) era igual que la del segundo número y el penúltimo (2+99), y así sucesivamente. Como había cien números, se formaban 50 parejas con la misma suma, es decir 101. Por lo que sólo faltaba multiplicar 101 x 50 = 5.050.
Giuseppe Piazzi, catedrático de astronomía en la Universidad de Palermo -Sicilia-, estaba buscando una estrella cuando a principios de 1801, cerca de la estrella que buscaba, vio un punto de luz que no coincidía con nada de lo que figuraba en los catálogos de estrellas. Siguió observándolo y se dio cuenta de que se movía. Lo llamó Ceres por la diosa romana de las cosechas, que también era la diosa patrona de Sicilia. Al principio pensaba que había descubierto un nuevo cometa, pero tenía la típica cola o cabellera así que se le pasó por la cabeza que podría ser un planeta.
Ceres es bastante pequeño para los estándares planetarios y lo perdió. Acumulaba muy pocos datos sobre su órbita y, antes de que pudiesen obtener más, el movimiento de la Tierra hizo que la visión de Ceres estuviese demasiado cerca del Sol, de modo que su débil luz fue anulada por el resplandor de este. Se esperaba que reapareciese unos meses más tarde, pero como se disponía de tan pocos datos, por donde divisarlo era un enigma. Para no empezar la búsqueda de nuevo, los astrónomos pidieron a la comunidad científica que les proporcionase una predicción de por donde buscar. Carl Friedrich Gauss, que en aquel entonces era muy poco conocido consiguió acertar el reto. Inventó un nuevo modo de deducir la órbita a partir de tres o más observaciones -ahora conocido como el método de Gauss. Cuando Ceres reapareció como debía con medio grado respecto a la posición pronosticada, Gauss empezó a ser considerado un gran matemático. A partir de este éxito, Gauss desarrolló una teoría completa sobre el movimiento de pequeños asteroides perturbados por planetas grandes. En este trabajo, Gauss mejoró un método estadístico introducido por Legendre en 1805, ahora llamado «método de los mínimos cuadrados» y que se utiliza muchísimo en estadística. También afirmó que había tenido la idea antes, en 1795, pero, como de costumbre, Gauss no la había publicado. Este método se emplea para deducir valores más precisos a partir de una serie de medidas sujetas a errores aleatorios -si quieres profundizar revisa la entrada en esta web sobre Data Science.
Dice la historia que en uno de los viajes de Tales de Mileto cuando estaba en Egipto, le preguntaron si sabría calcular la altura de la pirámide de Keops.
Lo que hizo Tales y que se conoce como el «Teorema de Tales» es clavar un bastón sobre el suelo junto a la pirámide. La sombra proyectada por la altura del bastón guarda proporción con la sombra proyectada por la pirámide así como la altura del bastón guarda proporción con la altura de la pirámide.
El último teorema de Fermat. Pierre de Fermat solia hacer notas en los márgenes de sus libros. La gente las tomaba como retos y, a través de los siglos, han sido resueltas todas ellas. Una de las notas que escribió en su libro de La Aritmética de Diofanto decía:
«No existen tres números enteros x, y, z -distintos de cero- que cumplan la ecuación $x^n + y^n = z^n , \forall n>2$ .He encontrado una demostración maravillosa para este teorema, pero este margen es demasiado estrecho para contenerla». El último teorema de Fermat fue demostrado por Andrew Willes en 1995 tras 10 años de decicarse a ello y utilizando matemáticas que no se conocían hasta el siglo XX por lo que no parece cierto que Fermat lo hubiese podido demostrar.