El problema de la mochila es un ejercicio típico de la rama de matemáticas que se llama «Investigación Operativa». Consiste en un excursionista que debe preparar su mochila, la cual tiene una capacidad limitada, esto hace que no pueda incluir todas las cosas que este en un primer momento querría llevar a la excursión.
Cada objeto que el excursionista quiere incluir en la mochila le reporta una determinada utilidad. El problema consiste en seleccionar el subconjunto de objetos que haga que se maximice la utilidad que el excursionista obtiene, pero sin superar la capacidad de peso máxima que admite la mochila.
Existen infinidad de ejemplos en la vida real conceptualmente similares al problema de la mochila, por lo que la creación de un modelo matemático que resuelva este problema se puede extrapolar a todos esos casos.
Por ejemplo, tener que enviar ayuda humanitaria en un avión a un país teniendo cada objeto a enviar un peso o volumen y un valor, lo mismo con un barco y contenedores, archivos de ordenador de distintos tamaño y un disco informático en el que almacenarlos con una capacidad limitada, en general, cualquier problema en el que sea necesario colocar artículos de diferente volumen en un espacio reducido, etc.
Matemáticamente, el caso más sencillo del problema podemos expresarlo como:
Sean:
$n$: Número de objetos distintos
$x_i$: Elemento i
$w_i$: Peso/volumen del elemento i
$b_j$: Beneficio/Valor del elemento i
$c$: Capacidad total de la mochila
y sean $c, w_i$ y $b_i$ enteros positivos
Podemos plantear el modelo como
Maximizar $\sum_{i=1}^{n}b_i x_i$
sujeto a $\sum_{i=1}^{n}w_i x_i \leq c$
Una solución a este problema -que pueden no ser óptima-, es ordenar los elementos de forma decreciente según esta proporción
$r_i=\frac{b_i}{w_i}$
y metiendo los elementos en la mochila hasta que ya no quepa ninguno.
Veamos un ejemplo:
| Elemento | Valor | Peso | Ratio |
| A | 200 | 40 | 5 |
| B | 80 | 20 | 4 |
| C | 30 | 15 | 2 |
| D | 15 | 20 | 0,75 |
| E | 10 | 80 | 0,125 |
Si la capacidad de la mochila es c=70, meteríamos los elementos A y B. ¡Ojo!, los elementos tenemos que ordenarlos por la ratio, si no lo estuvieran tendríamos que hacerlo.
Hay otras formas mejores de resolver este problema como son el método de Dantzig, el método de Martello yToth, etc. Un método que a mí me gusta bastante es la utilización de un algoritmo genético. Este tipo de algoritmos se utilizan mucho para resolver problemas de optimización.
Existen múltiples versiones del problema de la mochila, incluso se puede considerar el problema de tener varias mochilas con distintas capacidades.
Como ya he dicho, existen múltiples aplicaciones en la vida real en función de la limitación que se tenga (que no tiene que ser únicamente de peso o volumen), otros ejemplos pueden ser el desperdiciar la menor cantidad de tela -La cantidad de material es la limitación-, aprovechar al máximo el uso de máquinas excavadoras en una gran obra -el tiempo es el recurso limitante en este caso-.
Al principio de esta entrada he dicho que este es un problema típico de Investigación Operativa. El origen de la Investigación Operativa surgió durante la Segunda Guerra Mundial para dar respuesta a problemas del estilo de trasladar tropas al mínimo coste, diseño de la configuración optima de convoyes para minimizar la escolta y los daños en caso de ataque de un submarino, diseño de la configuración óptima de escuadrones de bombarderos, en definitiva para resolver problemas de asignación óptima de recursos. De aquí surgió el nombre, Investigación de Operaciones -militares-.
En este escenario surgió el «problema de la dieta», que consistía en minimizar los costes de la alimentación del ejército de los EEUU manteniendo garantizar unas cantidades mínimas de proteínas, carbohidratos, etc que deberían cumplirse por soldado. En este caso tenemos un listado del estilo: patatas, pan, tomates, etc y habría que obtener la ración óptima -más barata- por hombre, cumpliendo unas condiciones -restricciones-.
Tras la guerra, todo este conocimiento paso a usarse de forma civil, así el problema de la dieta se puede utilizar para alimentar al ganado, otros usos de la Investigación Operativa pasaron a ser la optimización de flujos en redes de gas, diseño de rutas de vehículos -el problema del cartero-, etc.
Dentro de la Investigación Operativa también se suele emplear mucho una técnica que se llama Programación Lineal.
La programación lineal es un método para maximizar -o minimizar- una cierta cantidad asegurando que se cumplen unas ciertas condiciones. Normalmente estas condiciones son lineales -sus gráficas son líneas rectas-, de aquí viene el nombre de «Programación lineal». Es una de las técnicas más útiles de la Investigación Operativa.
Supongamos que tenemos una empresa que fabrica lámparas de estudio y tenemos unos costes de 9000 euros -en máquinas, electricidad, etc y 15 euros por cada lámpara producida.
El coste/gasto «g» que tenemos viene dado por la fórmula $g = 15x + 9000$ donde $x$ es el número de lámparas de estudio producidas.
Si pensamos poner un precio de venta de cada lámparas de estudio de 25 euros , nuestros ingresos «i» vendrán dados por la ecuación $ i = 25x$ , donde $x$ es el número de lámparas de estudio vendidas.
Representando ambas ecuaciones sobre el mismo par de ejes coordenados
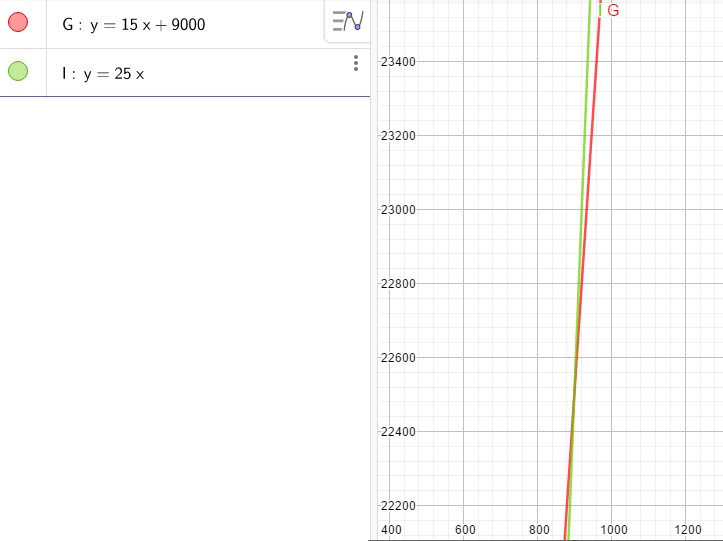
vemos que se cortan en un punto en el cual los gastos y los ingresos son iguales, o dicho de otra forma, el beneficio es 0 para x = 900 lámparas (g=i=22.500€) de modo que si vendemos menos de 900 lámparas, los costes superan los ingresos; si se venden más, los ingresos superan los costes; y si se venden exactamente 900 lámparas, tanto los ingresos como los costes son 22.500 euros. Maximizar los beneficios consiste en vender tantas lámparas como podamos y siempre más de 900.
Después de este sencillo ejemplo, veamos un caso más real de programación lineal.
Supongamos que una empresa fabrica dos tipos de taburetes. Producir un taburete caro cuesta 12€ y el precio de venta es de 30€, mientras que construir un taburete barato cuesta 5€. y se vende a 18€. La empresa no puede fabricar más de 300 taburetes al mes y no puede gastar más de 2.500€. al mes en su producción -son normas de la empresa ya que fabrica muchas más cosas.
Si la compañía ha de fabricar al menos 50 taburetes de cada tipo ¿cuántos ha de fabricar de cada clase para maximizar sus beneficios?
Si llamamos «x» al número de taburetes caros que la compañía fabrica cada mes e «y» al de taburetes caros, vemos que las condiciones sobre «x» e «y» del problema son:
$x+y \le 300$
$x \ge 50$
$y \ge 50$
$12x + 5y \le 2500$
Estas condiciones se cumplen en el área sombreada de negro.
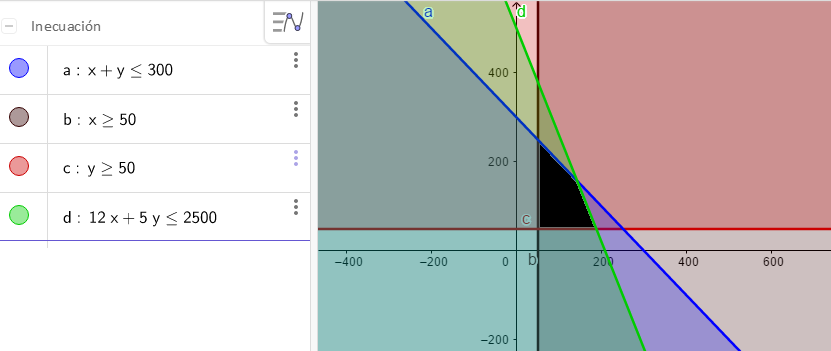
La cantidad que hay que maximizar es el beneficio, b = 18x + 13y. Esto es así porque el beneficio que se tiene por cada taburete caro es de 18€ (30€-12€) y por cada taburete barato 13€ (18€ -5€).
Una vez tenemos el problema planteado de esta forma, hay varias técnicas para hallar la solución. Una es gráfica y consiste en encontrar los vértices y los lados de la región permitida —nuestra zona sombreada de negro— y luego probarlas para encontrar en cuál de ellas se tiene el máximo beneficio. Con este método, y un poco de geometría analítica, descubrimos que la compañía de taburetes debería fabricar 143 taburetes caros (x) y 157 baratos (y) al mes para obtener el máximo beneficio.
Otra técnica, el método simplex, debida al matemático George Danzig, desarrolla y formaliza esta estrategia geométrica de forma que un ordenador pueda determinar estos puntos en el caso de que haya más de dos variables.

