El modelo de Markowitz consiste en dada una cartera de activos financieros, encontrar la cartera más adecuada para cada inversor en función del riesgo que éste esté dispuesto a asumir, o dicho de otra forma, dada una cartera o portafolio con «n» activos financieros, el modelo de Markowitz nos permite obtener los pesos asociados a esos activos de la forma más eficiente.
Por ejemplo para una cartera con cuatro activos
| Portafolio | Activo 1 | Activo 2 | Activo 3 | Activo 4 |
| 45% | 15% | 35% | 5% |
el modelo nos va a ayudar a decidir qué peso del dinero que vamos a invertir, deberíamos asignar a cada activo.
Con el modelo de Markowitz, podemos obtener los pesos asociados a los activos de la cartera en función del perfil de riesgo que cada persona tenga, naturalmente todos queremos la cartera que ofrezca la mayor rentabilidad esperada, pero si eso nos supone asumir un gran riesgo, puede que nos interese elegir la misma cartera, pero con otros pesos para esos activos, y que generándonos algo menos de rentabilidad nos suponga asumir un riesgo menor.
La finalidad de este artículo es ver cómo calcular estos pesos matemáticamente, y para ello lo vamos a hacer con un ejemplo sencillo de una cartera compuesta únicamente por dos activos.
Revisa la entrada de esta web titulada Estadística y fondos de inversión si quieres recordar conceptos como varianza, covarianza, etc., ya que los vamos a utilizar a continuación.
Supongamos que queremos configurar una cartera formada por dos activos «x» e «y», imaginemos que los que nos gustan son Telefónica y Repsol por decir algo, ¿qué peso del dinero del que disponemos debemos «colocar» en cada uno de ellos para tener una cartera optima?, si los pesos son $w_x$ y $w_y$, debe cumplirse que $w_x+w_y=1$ (es decir la suma de los pesos debe sumar 1 o el 100% si lo preferimos ver de forma porcentual).
Sean $ N_t$ y $N_{t-1}$ los precios (nav) de un activo para un periodo t y t-1, sabemos que podemos calcular su rentabilidad como $R_t=\frac{N_t – N_{t-1}}{N_{t-1}}$
Se define el Rendimiento Esperado o rentabilidad esperada de un activo como
$Re=\overline{R}=\frac{1}{n} \sum_{t=1}^{n} R_t$ , i.e. , es el promedio de los rendimientos en esos periodos.
La varianza $\sigma^2= \frac{1}{n-1} \sum_{t=1}^{n} (R_t – \overline{R} )^2 $
y el riesgo $\sigma$ como $\sqrt(\sigma^2)$
La Rentabilidad de mi cartera va a ser $R_{cartera}= w_x \overline{R_x} + w_y \overline{R_y}$
Siendo
$w_i$ El peso del activo «i» en la cartera -estos pesos es lo que quiero determinar-.
$\overline{R_i}$ la rentabilidad esperada del activo i
El riesgo viene dado por la fórmula de la desviación típica de una cartera que para el caso de dos activos es:
$\sigma=\sqrt( w_x^2\sigma_x^2 + w_y^2\sigma_y^2 + 2w_xw_y \sigma_{xy})$
$\sigma_i^2$ la varianza del activo i
$\sigma_{xy}$ la covarianza de los activos x e y
Observación: El riesgo para una cartera con tres activos sería:
$\sigma=\sqrt( w_x^2\sigma_x^2 + w_y^2\sigma_y^2++ w_z^2\sigma_z^2+ 2w_xw_y \sigma_{xy} + 2w_xw_z \sigma_{xz} + 2w_yw_z \sigma_{yz} )$. Para el caso de «n» activos se seguiría la misma lógica.
Veamos un ejemplo
| Precios | Rentabilidades esperadas | |||
| Activo x | Activo y | $R_x$ | $R_y$ | |
| día 1 | 35 | 50 | ||
| día 2 | 40 | 47 | 0,14285714 | -0,06 |
| día 3 | 37 | 50 | -0,075 | 0,063829787 |
| día 4 | 41 | 49 | 0,10810811 | -0,02 |
| día 5 | 42 | 54 | 0,02439024 | 0,102040816 |
siendo
$\overline{R_x}=0,050088874 = 5,00\%$ (rendimiento esperado del activo x)
$\overline{R_y}=0,021467651 = 2,14\%$
$\sigma_x^2 = 0,00942661=$ (varianza del activo x)
$\sigma_y^2 = 0,00554771$
$\sigma_x =0,0970 = 9,70\%$ (desviación típica del activo x, i.e., el riesgo)
$\sigma_y = 0,0744 = 7,44\%$
$\sigma_{xy} = -0,005776 $ (covarianza)
Con estos valores construyamos un primer portafolio en el que invertimos el 50% del capital en cada activo. En este caso, tendríamos la siguiente rentabilidad y riesgo para nuestra cartera:
$R_{P}= 50 \cdot \overline{R_x} + 50 \cdot \overline{R_y}$
$R_{P}= 50 \cdot 0,050088874 + 50 \cdot 0,021467651 = 3,57782623 = 3,57%$
$\sigma_P^2 = 0,5^2 \cdot 0,00942661 + 2 \cdot 0,5 \cdot 0,5 \cdot (-0,005776) + 0,5^2 \cdot 0,00554771 = 0,000854 $
$\sigma_P = \sqrt(0,000854) = 2,92\%$
Creando carteras similares variando los pesos tenemos:
| Portafolio | Peso activo x | Peso activo y | Riesgo en % | Rentabilidad en % |
| 1 | 0,05 | 0,95 | 6,69 | 2,28 |
| 2 | 0,1 | 0,9 | 5,95 | 2,42 |
| 3 | 0,15 | 0,85 | 5,23 | 2,56 |
| 4 | 0,2 | 0,8 | 4,55 | 2,71 |
| 5 | 0,25 | 0,75 | 3,92 | 2,85 |
| 6 | 0,3 | 0,7 | 3,37 | 2,99 |
| 7 | 0,35 | 0,65 | 2,94 | 3,14 |
| 8 | 0,4 | 0,6 | 2,7 | 3,28 |
| 9 | 0,45 | 0,55 | 2,69 | 3,42 |
| 10 | 0,5 | 0,5 | 2,92 | 3,57 |
| 11 | 0,55 | 0,45 | 3,33 | 3,71 |
| 12 | 0,6 | 0,4 | 3,88 | 3,85 |
| 13 | 0,65 | 0,35 | 4,5 | 3,99 |
| 14 | 0,7 | 0,3 | 5,18 | 4,14 |
| 15 | 0,75 | 0,25 | 5,9 | 4,28 |
| 16 | 0,8 | 0,2 | 6,63 | 4,42 |
| 17 | 0,85 | 0,15 | 7,38 | 4,57 |
| 18 | 0,9 | 0,1 | 8,15 | 4,71 |
| 19 | 0,95 | 0,05 | 8,92 | 4,85 |
Lo que nos da un gráfico de dispersión entre el rendimiento y el riesgo como el siguiente (con MS Excel se pinta el gráfico perféctamente):
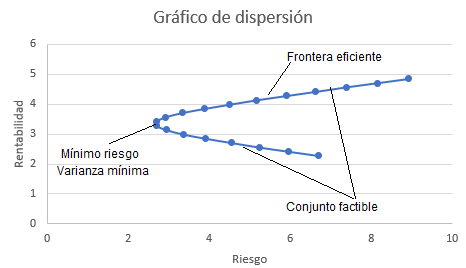
Variando los pesos podemos tener un número infinito de portafolios.
Markowitz denomina Conjunto Factible a la gráfica resultante de dibujar las distintas combinaciones entre el riesgo y la rentabilidad de la cartera. Es la línea azul del gráfico anterior.
Como el eje de abscisas es el riesgo, el punto más a la izquierda es el punto de mínimo riesgo. A patir de ahí, hay portafolios que se encuentran por encima y son los que conforman la Frontera Eficiente. A medida que nos movemos por el eje de abscisas hacia la derecha aumenta el riesgo y le corresponden dos puntos de la curva (flecha verde y flecha roja), está claro que a igual riesgo, de las dos posibles rentabilidades que nos puede dar la cartera para ese riesgo fijado, lo que tenemos que hacer es quedarnos con el punto de la flecha verde, es decir, con aquella que se encuentra en la frontera eficiente puesto que ahí la rentabilidad es mayor.
La Frontera Eficiente es el conjunto de las carteras más eficientes de todo el universo de carteras que se puede encontrar con una combinación de activos determinada.
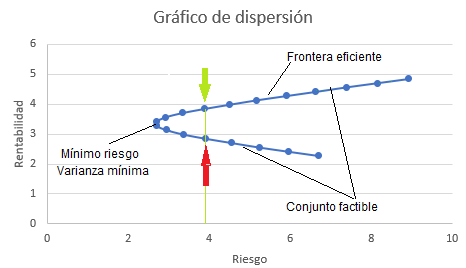
Al portafolio de mínimo riesgo se le denomina Portafolio Óptimo.
La varianza de nuestra cartera ya vimos que venia dada por la fórmula
$\sigma^2= w_x^2\sigma_x^2 + w_y^2\sigma_y^2 + 2w_xw_y \sigma_{xy}$
que es la suma de tres términos y en la que podemos observar que si la covarianza $\sigma_{xy}$ es negativa, el riesgo de mi cartera es menor que si ésta es positiva.
El problema matemático de optimización para encontrar el portafolio óptimo, consiste en encontrar los pesos $w_x$ y $w_y$ tales que la varianza -riesgo- sea mínima siendo $w_x + w_y = 1$, es decir.
$\begin{cases}\text{Mínimo de la varianza } \sigma^2= \text {Mínimo de la función } f(w_x, w_y)= w_x^2\sigma_x^2 + w_y^2\sigma_y^2 + 2w_xw_y \sigma_{xy} \\ w_x + w_y = 1 \end{cases}$
Este problema podemos resolverle a través del método de los multiplicadores de Lagrange que nos permite encontrar los máximos y mínimos de funciones de múltiples variables sujetas a restricciones.
En nuestro caso la función de Lagrange $h$ sería:
$h(w_x, w_y,\lambda)= w_x^2\sigma_x^2 + 2w_xw_y \sigma_{xy} +w_y^2\sigma_y^2 + \lambda (1-w_x – w_y)$
Procedemos a igualar sus derivadas parciales a 0 para encontrar los puntos críticos (en este caso un mínimo).
$\begin{cases}\frac{\partial h}{\partial w_x} = 2 w_x \sigma_x^2 +2w_y \sigma_{xy} – \lambda =0 \\ \frac{\partial h}{\partial w_y} = 2 w_y \sigma_y^2 +2w_x \sigma_{xy} – \lambda=0 \\ \frac{\partial h}{\partial \lambda}= 1 – w_x – w_y =0 \end{cases}$
Si resolviesemos estes sistema de tres ecuaciones llegaríamos al resultado
$w_x =\frac{\sigma_y^2 – \sigma_{xy} }{\sigma_x^2 +\sigma_y^2 – 2 \sigma_{xy}}$
$w_y=1-w_x$
habiendo llegado por tanto a obtener los pesos de la cartera óptima que volviendo al caso de nuestro ejemplo serían:
$w_x=\frac{0,005544 -(-0,005776) }{0,0009424 +0,005544 – 2 \cdot (-0,005776) }=0,4268=42,68\%$
$w_y=1-w_x=1-0,4268=0,5732=57,32\%$
Para estos pesos la rentabilidad esperada es del 3,36% y el riesgo o volatilidad del 2,66%.
Off topic al método de Markowitz que acabamos de ver, en el caso de tener una cartera de fondos de inversión y una vez decididos los fondos $F_1, F_2, …, F_n$ que quiero incorporar a la misma, una herramienta que no conozco que exista en el mercado, sencilla de construir -si trabajas en un banco que se dedica a los fondos de inversión y por tanto tienes la materia prima que son los valores liquidativos de estos- y realmente útil, sería la que siguiese el siguiente algoritmo:
Para cada fondo $F_i$ que queremos incorporar a la cartera, obtener todos los fondos de inversión de su misma categoría -activo y zona geográfica- que hayan tenido mejor rentabilidad en los últimos tres años que $F_i$, con una volatilidad inferior a la de $F_i$ también en los últimos tres años y los mostraríamos ordenados por:
Rentabilidad de mayor a menor y luego ordenados por el ratio de Sharpe de mayor a menor.
Esto solo lo haríamos para fondos traspasables.
No he tenido en cuenta -en esta primera versión- dividendos ni comisiones, pero se podrían incorporar éstos al algoritmo anteriormente descrito.
Con esto obtendríamos una cartera similar a la que habíamos elegido en primera instancia, pero mejorada. Si una vez elegidos los fondos de esta forma, aplicasemos Markowitz para la elección de los pesos, pues tendríamos la cartera «galáctica» amoldada a nuestro gusto de tipo de fondos (asset allocation).